वृत्तों के एक निकाय में, प्रत्येक दो वृत्त जिनके मूलाक्ष समान हो समाक्ष कहे जाते है।
समाक्ष वृत्त निकाय का व्यापक समीकरण x2+y2+2gx+c=0 है। जहाँ g भिन्न-भिन्न वृत्त निकाय के लिए भिन्नात्मक है तथा c सभी वृत्तों के लिए समान है, उभयनिष्ठ मूलाक्ष y-अक्ष तथा केन्द्रों की रेखा x-अक्ष है।
मूलाक्ष के दिए गये समीकरण तथा निकाय S=0 के एक वृत्त को रखने वाले समाक्ष वृत्त निकाय का समीकरण S=λu=0 है। दिए गये निकाय के दो वृत्तों के समीकरणों
S1=x2+y2+2g1x+2f1y+c1=0
S2=x2+y2+2g2x+2f2y+c2=0 को रखने वाले समाक्ष वृत्त निकाय का समीकरण S1+λS2=0 है।।
समाक्ष वृत्त निकाय के सदस्यों जो शून्य त्रिज्या के हैं निकाय के सीमान्त बिन्दु कहे जाते हैं।
वृत्ते x2+y2−2x−6y+9=0 तथा x2+y2+6x−2y+1=0 के द्वारा ज्ञात किए गए समाक्ष निकायों के सीमांत बिन्दु हैं
(−1,2),(35,−145)
(−1,2),(35,145)
(−1,2),(−35,145)
इनमें से कोई नहीं
The correct Answer is:B
Step by step video, text & image solution for वृत्तों के एक निकाय में, प्रत्येक दो वृत्त जिनके मूलाक्ष समान हो समाक्ष कहे जाते है। समाक्ष वृत्त निकाय का व्यापक समीकरण x^(2)+y^(2)+2g x+c=0 है। जहाँ g भिन्न-भिन्न वृत्त निकाय के लिए भिन्नात्मक है तथा c सभी वृत्तों के लिए समान है, उभयनिष्ठ मूलाक्ष y-अक्ष तथा केन्द्रों की रेखा x-अक्ष है। मूलाक्ष के दिए गये समीकरण तथा निकाय S=0 के एक वृत्त को रखने वाले समाक्ष वृत्त निकाय का समीकरण S= lambda u=0 है। दिए गये निकाय के दो वृत्तों के समीकरणों S_(1)=x^(2)+y^(2)+2g_(1)x+2f_(1)y+c_(1)=0 S_(2)=x^(2)+y^(2)+2g_(2)x+2f_(2)y+c_(2)=0 को रखने वाले समाक्ष वृत्त निकाय का समीकरण S_(1)+lambdaS_(2)=0 है।। समाक्ष वृत्त निकाय के सदस्यों जो शून्य त्रिज्या के हैं निकाय के सीमान्त बिन्दु कहे जाते हैं।वृत्ते x^(2) +y^(2)-2x-6y+9 = 0 तथा x^(2) + y^(2) +6x-2y+1 = 0 के द्वारा ज्ञात किए गए समाक्ष निकायों के सीमांत बिन्दु हैं by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- वृत्त तथा वृत्तों का निकाय BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - JEE Advanced (Matrix Match type questions)
8 Videos
- वृत्त तथा वृत्तों का निकाय BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - Solved Multiple Choice Questions (वृत्त का समीकरण, वृत्त से सम्बंधित ज्यामितीय प्रश्न)
122 Videos
- वृत्त तथा वृत्तों का निकाय BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - JEE Advanced (Reasoning type questions )
8 Videos
- वर्ग समीकरण एवं असमिकायें BOOK - ERRORLESS HINDICHAPTER - वर्ग समीकरण एवं असमिकायें EXERCISE - JEE Advanced (Matrix Match type questions)
2 Videos
- शांकव परिच्छेद BOOK - ERRORLESS HINDICHAPTER - शांकव परिच्छेद EXERCISE - JEE Advanced (Matrix Match type questions)
7 Videos
Similar Questions
कॉलम I में दिए गए वक्त्तव्यों का कॉलम II में दिए गए गुणधर्मों से सुमेल करें
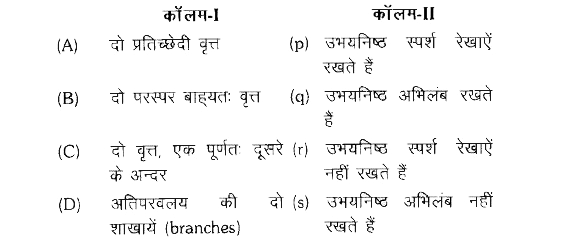
View Solutionवृत्त x2+y2−2x+4y+3=0 के अंतर्गत एक वर्ग खींचा गया है जिसकी भुजायें निर्देशांक अक्षों के समान्तर है। तब बर्ग का एक शीर्ष है
View Solutionमाना L1=2x+3y+p−3=0,L2:2x+3y+p+3=0
जहाँ p एक वास्तविक संख्या है तथा C=x2+y2+6x−10y+30=0
कथन-1 : यदि रेखा L1 वृत्त C की जीवा है, तब रेखा L2 सदैव वृत्त C का व्यास नही होगी तथा
कथन-2 : यदि रेखा L1 वृत्त C का व्यास है, तब रेखा L2 वृत्त C की जीवा नहीं होगी।
View Solution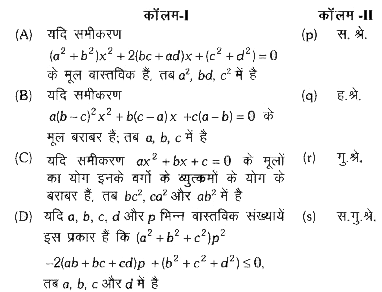
View Solution
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionदर्शाइए की बिंदु x=2at1+t2 तथा y=a(1−t2)1+t2 जहाँ a स्थिर राशि है t प्राचल है तथा −1≤t≤1,t के प्रत्येक मान के लिए वृत्त पर स्थित है ।
View Solutionk के सभी मानो के लिए वृत्त x2+y2−kx−2ky+k2=0 स्पर्श करता है -
View Solutionरेखा तथा वृत्त के स्पर्श बिंदु के निर्देशांक ……………. है ।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (a,b,c) से होकर जाती है तथा Y-अक्ष के समान्तरहै।
View SolutionY - अक्ष के समीकरण का सममित रूप …………. है।
View Solutionλ के किस मान के लिए निम्न समीकरण के निकाय
2x−y−2z=2,x−2y+z=−4,x+y+λz=4 का कोई हल नहीं है
View Solutionयदि निकाय के समीकरणों x−ky−z=0,kx−y−z=0 तथा x+y−z=0 का एक अशून्य हल है, तो k का संभावित मान होगा
View Solutionयदि समीकरण निकाय x+ay=0,ax+y=0 और ax+z=0 के अनंत हल है, तब a का मान है
View Solutionc∈R का अधिकतम मान, जिसके लिए रेखिक समीकरण निकाय x−cy−cz=0,cx−y+cz=0,cx+cy−z=0 का एक अत्युच्च हल है, है
View Solution
