Two bombs of 5 kg and 10 kg are thrown from a cannon with the same velocity in the same direction,If the bombs are thrown in the same direction with different velocity, what would be the effect ?
To analyze the effect of throwing two bombs of different masses (5 kg and 10 kg) with different velocities but in the same direction, we can break down the problem into several key components: time of flight, range, and maximum height.
1. Understanding Time of Flight:
The time of flight (T) for a projectile is given by the formula:
T=2usinθg
where u is the initial velocity, θ is the angle of projection, and g is the acceleration due to gravity.
- For the 5 kg bomb thrown with velocity u:
T5=2usinθg
- For the 10 kg bomb thrown with velocity v:
T10=2vsinθg
Since u and v are different, the time of flight will differ for the two bombs.
2. Calculating the Range:
The range (R) of a projectile is given by:
R=u2sin2θg
- For the 5 kg bomb:
R5=u2sin2θg
- For the 10 kg bomb:
R10=v2sin2θg
Again, since u and v are different, the ranges will also differ.
3. Finding the Maximum Height:
The maximum height (H) reached by a projectile is given by:
H=u2sin2θ2g
- For the 5 kg bomb:
H5=u2sin2θ2g
- For the 10 kg bomb:
H10=v2sin2θ2g
The maximum height will also change based on the different initial velocities.
Conclusion:
In summary, when the two bombs are thrown in the same direction but with different velocities, the following effects are observed:
- Time of Flight: Different for each bomb due to different initial velocities.
- Range: Different distances covered by each bomb based on their respective velocities.
- Maximum Height: Different heights achieved by each bomb based on their respective velocities.
The time of flight (T) for a projectile is given by the formula:
T=2usinθg
where u is the initial velocity, θ is the angle of projection, and g is the acceleration due to gravity.
- For the 5 kg bomb thrown with velocity u:
T5=2usinθg
- For the 10 kg bomb thrown with velocity v:
T10=2vsinθg
Since u and v are different, the time of flight will differ for the two bombs.
The range (R) of a projectile is given by:
R=u2sin2θg
- For the 5 kg bomb:
R5=u2sin2θg
- For the 10 kg bomb:
R10=v2sin2θg
Again, since u and v are different, the ranges will also differ.
The maximum height (H) reached by a projectile is given by:
H=u2sin2θ2g
- For the 5 kg bomb:
H5=u2sin2θ2g
- For the 10 kg bomb:
H10=v2sin2θ2g
The maximum height will also change based on the different initial velocities.
In summary, when the two bombs are thrown in the same direction but with different velocities, the following effects are observed:
- Time of Flight: Different for each bomb due to different initial velocities.
- Range: Different distances covered by each bomb based on their respective velocities.
- Maximum Height: Different heights achieved by each bomb based on their respective velocities.
Topper's Solved these Questions
Similar Questions
Knowledge Check
All the particles thrown with same initial velocity would strike the ground.
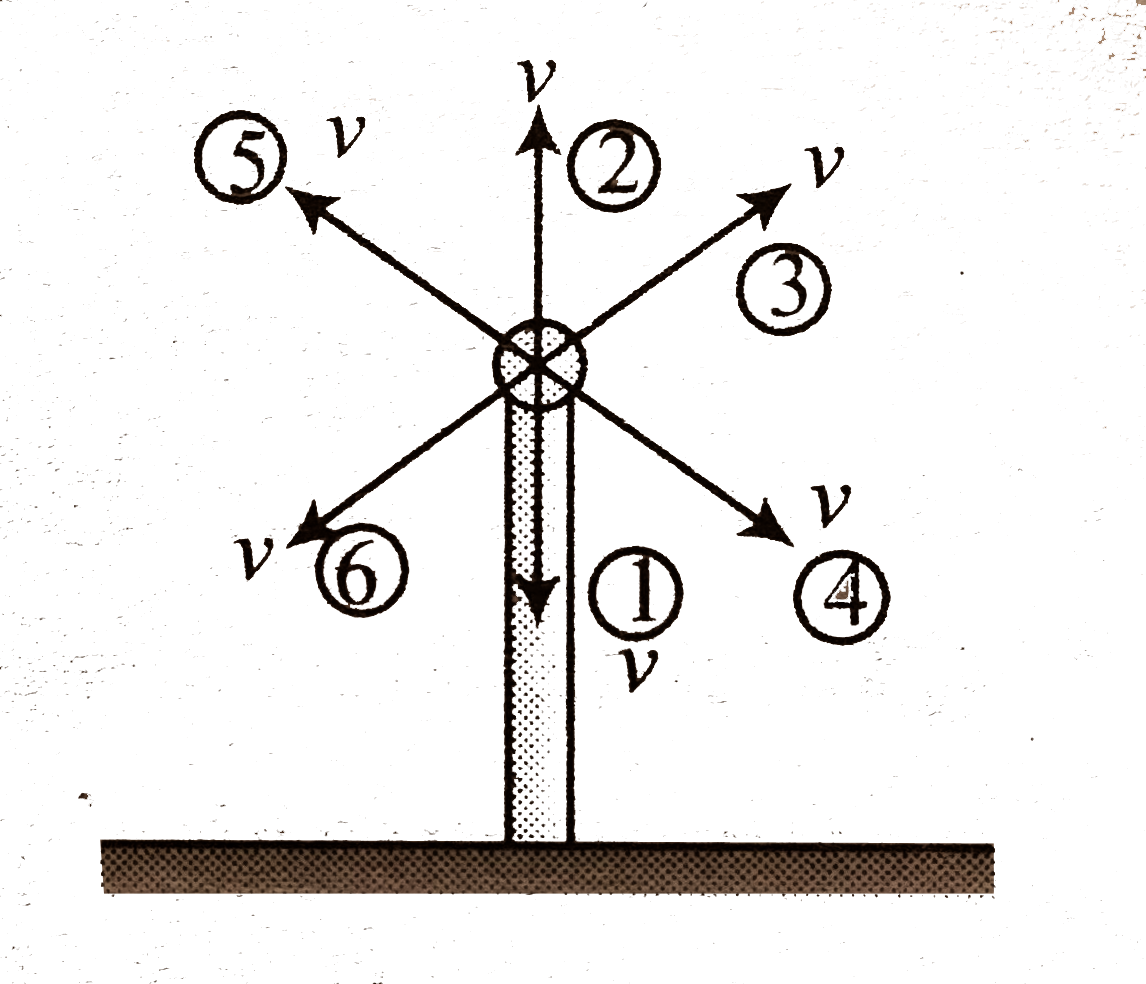 .Awith same speed.BsimultaneouslyCtime would be least for the particle thrown with velocity v downward i.e., particle 1.Dtime would be maximum for the particle 2.
.Awith same speed.BsimultaneouslyCtime would be least for the particle thrown with velocity v downward i.e., particle 1.Dtime would be maximum for the particle 2.A body of mass 5 kg is moving with a velocity 20m/s. If a force of 100 N is applied on it for 10s in the same direction as its velocity what will be the velocity of the body?
A180m/sB200m/sC220m/sD250 m/sA body of 5kg is moving with a velocity of 20m/s. If a force of 100N is applied on it for 10 s in the same direction as its velocity, what will now be the velocity of the body?
A2000m/sB220m/sC240m/sD260m/s
Two bodies of masses 4 kg and 6 kg are thrown with the same velocity in the same direction . Which body will reach the ground first ?
View SolutionWhen are the diplacement and velocity in the same direction in SHM?
View SolutionWhen are the velocity and acceleration in the same direction SHM?
View SolutionWrite two different vectors having same direction.
View SolutionWrite two different vectors having same direction.
View Solution

