A horizontal stream of water leaves an opening in the side of a tank. If the opening is h metre above the ground and the stream hits the round D metre away, then what is the speed of water as it leaves the tank in terms of g, h and D ?
To solve the problem of finding the speed of water as it leaves the tank in terms of g, h, and D, we can follow these steps:
Step 1: Understand the motion of the water stream
The water leaves the tank horizontally from a height h and travels a horizontal distance D before hitting the ground. The motion can be analyzed in two components: horizontal and vertical.
Step 2: Analyze the vertical motion
Since the water is falling under the influence of gravity, we can use the second equation of motion for the vertical displacement:
h=ut+12gt2
Here, u is the initial vertical velocity (which is 0 since the water leaves horizontally), g is the acceleration due to gravity, and t is the time of flight.
Substituting u=0:
h=0⋅t+12gt2⟹h=12gt2
Step 3: Solve for time t
Rearranging the equation gives:
t2=2hg⟹t=√2hg
Step 4: Analyze the horizontal motion
The horizontal distance D traveled by the water stream can be expressed as:
D=vt
where v is the horizontal speed of the water as it leaves the tank.
Step 5: Substitute for time t
Now, substituting the expression for t from Step 3 into the horizontal motion equation:
D=v⋅√2hg
Step 6: Solve for the speed v
Rearranging the equation to solve for v:
v=D√2hg
This can be simplified further:
v=D⋅√g2h
Final Result
Thus, the speed of water as it leaves the tank in terms of g, h, and D is:
v=D√g2h
The water leaves the tank horizontally from a height h and travels a horizontal distance D before hitting the ground. The motion can be analyzed in two components: horizontal and vertical.
Since the water is falling under the influence of gravity, we can use the second equation of motion for the vertical displacement:
h=ut+12gt2
Here, u is the initial vertical velocity (which is 0 since the water leaves horizontally), g is the acceleration due to gravity, and t is the time of flight.
h=0⋅t+12gt2⟹h=12gt2
Rearranging the equation gives:
t2=2hg⟹t=√2hg
The horizontal distance D traveled by the water stream can be expressed as:
D=vt
where v is the horizontal speed of the water as it leaves the tank.
Now, substituting the expression for t from Step 3 into the horizontal motion equation:
D=v⋅√2hg
Rearranging the equation to solve for v:
v=D√2hg
This can be simplified further:
v=D⋅√g2h
Thus, the speed of water as it leaves the tank in terms of g, h, and D is:
v=D√g2h
Topper's Solved these Questions
Similar Questions
A stream of water escapes from a hole 2m above the Q. 1 base of a tank and strikes the ground at a horizontal distance of 6m .The depth of the hole from the free surface of water is
View SolutionA stream of water escapes from a hole 2m above the Q. 1 base of a tank and strikes the ground at a horizontal distance of 6m .The depth of the hole from the free surface of water is
View Solution
Knowledge Check
Water is flowing through a horizontal pipe fixed at a height of 2 m above the ground as shown in Fig. 5.90. water strikes ground at a distance of 3m from the pipe. The speed of water as it leaves the pipe is:
 A47m/sB4.7m/sC9.4m/sD4.9m/s
A47m/sB4.7m/sC9.4m/sD4.9m/sAn open water tank has an orifice 10 cm below the surface of water. If there is no loss of energy, then what is the speed of efflux ? (Take g = 10 m s−2)
A1.414 m s−1B2.5 m s−1C6.32 m s−1D3.7 m s−1A tank, which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank :
 A2√h(H−h)B√h(H−h)C2√h2H−hD√h2H−h
A2√h(H−h)B√h(H−h)C2√h2H−hD√h2H−h
A stream of water escapes from a hole 2m above the base of a tank and strikes the ground at a horizontal distance of 6m .The depth of the hole from the free surface of water is
View SolutionIn the old West , a desperado fires a bullet into an open water tank Fig , creating a hole a distance h below the water surface . What is the speed v of the water exiting the tank ?

View SolutionWater is filled in tank 3 m height. The base of the tank is at height 1 m above the ground. What should be the height of a hole made in it, so that water can be sprayed upto maximum horizontal distance on ground?
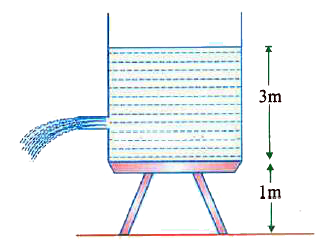
View SolutionA tank is filled with water up to a height H. Water is allowed to come out of a hole P in one of the walls at a depth D below the surface of water. Express the horizontal distance x in terms of H and D
 .
.
View SolutionA large tank is filled with water to a depth of 15 m . A spout located 10.0 m above the bottom of the tank is then opened as shown in the figure . With what speed will water emerge from the spout ?

View Solution
