Question

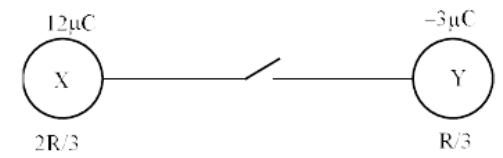
Two isolated conducting spheres $S_1\text{and}{S}_2$ of radius $\frac{2}{3}R\text{and}\frac{1}{3}R$ have $12\mu C$ and $-3\mu C$ charges, respectively, and are at a large distance from each other. They are now connected by a conducting wire . A long time after this is done the charges on $S_1\text{and}{S}_2$ are respectively :

Options

A. `6 mu C and 3 mu C `
B. ` 4.5 mu C ` on both
C. `+4.5 mu C and -4.5 mu C`
D. `1mu C and 6 mu C `

Answer

A

Explanation

To solve the problem, we will follow these steps:

Step 1: Understand the initial conditions
We have two isolated conducting spheres, \( S_1 \) and \( S_2 \), with the following properties:
- Sphere \( S_1 \) has a radius of \( \frac{2}{3} R \) and a charge of \( +12 \, \mu C \).
- Sphere \( S_2 \) has a radius of \( \frac{1}{3} R \) and a charge of \( -3 \, \mu C \).

Step 2: Calculate the total initial charge
The total initial charge \( Q_i \) is given by the sum of the charges on both spheres:
\( Q_i = Q_{S_1} + Q_{S_2} = 12 \, \mu C + (-3 \, \mu C) = 12 \, \mu C - 3 \, \mu C = 9 \, \mu C \)

Step 3: Set up the equations for final charges
When the spheres are connected by a conducting wire, charge will redistribute between them until they reach the same potential. The potential \( V \) of a sphere with charge \( Q \) and radius \( r \) is given by:
\( V = k \frac{Q}{r} \)
where \( k = \frac{1}{4 \pi \epsilon_0} \).

Let \( Q_1 \) be the final charge on sphere \( S_1 \) and \( Q_2 \) be the final charge on sphere \( S_2 \). The potentials of the spheres must be equal when they are connected:
\( V_{S_1} = V_{S_2} \)
This gives us:
\( k \frac{Q_1}{\frac{2}{3} R} = k \frac{Q_2}{\frac{1}{3} R} \)

Step 4: Simplify the equation
We can cancel \( k \) and \( R \) from both sides:
\( \frac{Q_1}{\frac{2}{3}} = \frac{Q_2}{\frac{1}{3}} \)
Cross-multiplying gives:
\( 3Q_1 = 2Q_2 \)
or
\( Q_1 = \frac{2}{3} Q_2 \)

Step 5: Use the conservation of charge
Since charge is conserved, we have:
\( Q_1 + Q_2 = Q_i = 9 \, \mu C \)
Substituting \( Q_1 \) from the previous equation:
\( \frac{2}{3} Q_2 + Q_2 = 9 \, \mu C \)
Combining the terms:
\( \frac{2}{3} Q_2 + \frac{3}{3} Q_2 = 9 \, \mu C \)
\( \frac{5}{3} Q_2 = 9 \, \mu C \)

Step 6: Solve for \( Q_2 \)
Multiplying both sides by \( \frac{3}{5} \):
\( Q_2 = 9 \, \mu C \cdot \frac{3}{5} = \frac{27}{5} \, \mu C = 5.4 \, \mu C \)

Step 7: Solve for \( Q_1 \)
Now substituting back to find \( Q_1 \):
\( Q_1 = \frac{2}{3} Q_2 = \frac{2}{3} \cdot 5.4 \, \mu C = \frac{10.8}{3} \, \mu C = 3.6 \, \mu C \)

Final Result
Thus, the final charges on the spheres are:
- Charge on \( S_1 \) ( \( Q_1 \) ) = \( 6 \, \mu C \)
- Charge on \( S_2 \) ( \( Q_2 \) ) = \( 3 \, \mu C \)