Two insulated charged conducting spheres of radii 20cm and 15cm respectively and having an equal charge of 10C are connected by a copper wire and then they are separted. Then
Both spheres will have equal charges
Surgace charge density on the 20 cm sphere will be greater than that on the 15 cm sphere
Surface charge density on the 15 cm sphere cm will be greater than that on the 20 cm sphere
Surface charge density on the two spheres will be equal .
To solve the problem, we will follow these steps:
Step 1: Understand the Problem
We have two insulated charged conducting spheres with radii R1=20cm=0.2m and R2=15cm=0.15m, each having a charge Q=10C. They are connected by a copper wire, allowing charge to redistribute until they reach the same potential.
Step 2: Calculate the Capacitance of Each Sphere
The capacitance C of a conducting sphere is given by the formula:
C=4πϵ0R
where ϵ0 is the permittivity of free space (ϵ0≈8.85×10−12F/m).
Calculating for both spheres:
- For Sphere 1 (radius R1=0.2m):
C1=4πϵ0R1=4π(8.85×10−12)(0.2)≈2.23×10−11F
- For Sphere 2 (radius R2=0.15m):
C2=4πϵ0R2=4π(8.85×10−12)(0.15)≈1.67×10−11F
Step 3: Calculate the Total Charge and Equivalent Capacitance
The total charge Qtotal when the spheres are connected is:
Qtotal=Q1+Q2=10C+10C=20C
The equivalent capacitance Cnet when the spheres are connected in parallel is:
Cnet=C1+C2≈2.23×10−11+1.67×10−11≈3.90×10−11F
Step 4: Calculate the Common Potential
The common potential Vc across both spheres when connected is given by:
Vc=QtotalCnet=20C3.90×10−11F≈5.13×1011V
Step 5: Calculate the Charge on Each Sphere After Separation
After they are separated, the charge on each sphere can be calculated using:
Q1=C1⋅VcandQ2=C2⋅Vc
Calculating Q1:
Q1=C1⋅Vc=2.23×10−11⋅5.13×1011≈11.43C
Calculating Q2:
Q2=C2⋅Vc=1.67×10−11⋅5.13×1011≈8.57C
Step 6: Analyze Surface Charge Densities
The surface charge density σ is given by:
σ=QA=Q4πR2
Calculating surface charge densities:
- For Sphere 1:
σ1=Q14πR21=11.434π(0.2)2≈45.25C/m2
- For Sphere 2:
σ2=Q24πR22=8.574π(0.15)2≈76.73C/m2
Conclusion
From the calculations:
- The charge on Sphere 1 is approximately 11.43C and on Sphere 2 is approximately 8.57C.
- The surface charge density on Sphere 2 is greater than that on Sphere 1.
Final Answer
The correct option is that the surface charge density on the 15 cm sphere will be greater than that on the 20 cm sphere.
---
We have two insulated charged conducting spheres with radii R1=20cm=0.2m and R2=15cm=0.15m, each having a charge Q=10C. They are connected by a copper wire, allowing charge to redistribute until they reach the same potential.
The capacitance C of a conducting sphere is given by the formula:
C=4πϵ0R
where ϵ0 is the permittivity of free space (ϵ0≈8.85×10−12F/m).
- For Sphere 1 (radius R1=0.2m):
C1=4πϵ0R1=4π(8.85×10−12)(0.2)≈2.23×10−11F
C2=4πϵ0R2=4π(8.85×10−12)(0.15)≈1.67×10−11F
The total charge Qtotal when the spheres are connected is:
Qtotal=Q1+Q2=10C+10C=20C
Cnet=C1+C2≈2.23×10−11+1.67×10−11≈3.90×10−11F
The common potential Vc across both spheres when connected is given by:
Vc=QtotalCnet=20C3.90×10−11F≈5.13×1011V
After they are separated, the charge on each sphere can be calculated using:
Q1=C1⋅VcandQ2=C2⋅Vc
Calculating Q1:
Q1=C1⋅Vc=2.23×10−11⋅5.13×1011≈11.43C
Calculating Q2:
Q2=C2⋅Vc=1.67×10−11⋅5.13×1011≈8.57C
The surface charge density σ is given by:
σ=QA=Q4πR2
Calculating surface charge densities:
- For Sphere 1:
σ1=Q14πR21=11.434π(0.2)2≈45.25C/m2
- For Sphere 2:
σ2=Q24πR22=8.574π(0.15)2≈76.73C/m2
From the calculations:
- The charge on Sphere 1 is approximately 11.43C and on Sphere 2 is approximately 8.57C.
- The surface charge density on Sphere 2 is greater than that on Sphere 1.
The correct option is that the surface charge density on the 15 cm sphere will be greater than that on the 20 cm sphere.
Similar Questions
Two insulated charges conducting spheres of radii 20 cm and 15 cm respectively and having an equal charge of 10μC are connected by a copper wire and then they are separated . Then
(1) Both spheres will have equal charges.
(2) Surface charges density on the 20 cm sphere will be greater than that on the 15 cm sphere
(3) Surface charge density on the 15 cm sphere will greater than that on the 20 cm sphere
(4) Surface charge density on the two spheres will be equal.
View SolutionTwo isolated sphereical conductors have radii 5cm and 10cm, espctively They have charges of 12μC and −3μC. Find the charges after they are connected by a conductng wire. Also find the common potential after resistribution.
View SolutionConsider Two metallic charged sphere whose radii are 20 cm and 10 cm respectively each having 150 microcoulomb positive charge. What is their common potential after they are connected by a conducting wire ?
View SolutionTwo isolated metallic spheres of radii 2 cm and 4 cm are given equal charge, then the ratio of charge density on the surfaces of the spheres will be
View SolutionTwo isolated sphereical conductors have radii 5cm and 0cm, espctively They have charges of 12μC and −3μC. Find the charges after they are connected by a conductng wire. Also find the common potential after resistribution.
View SolutionIn a conducting hollow sphere of inner and outer radii 5 cm and 10 cm, respectively, a point charge 1 C is placed at point A, that is 3 cm from the center C of the hollow sphere. An external uniform electric field to magnitude 20NC−1 is also applied. Net electric force on this charge is 15 N, away from the center of the sphere as shown. Find the magnitude of net force exerted on the charge placed at point A by the induced charges on the sphere
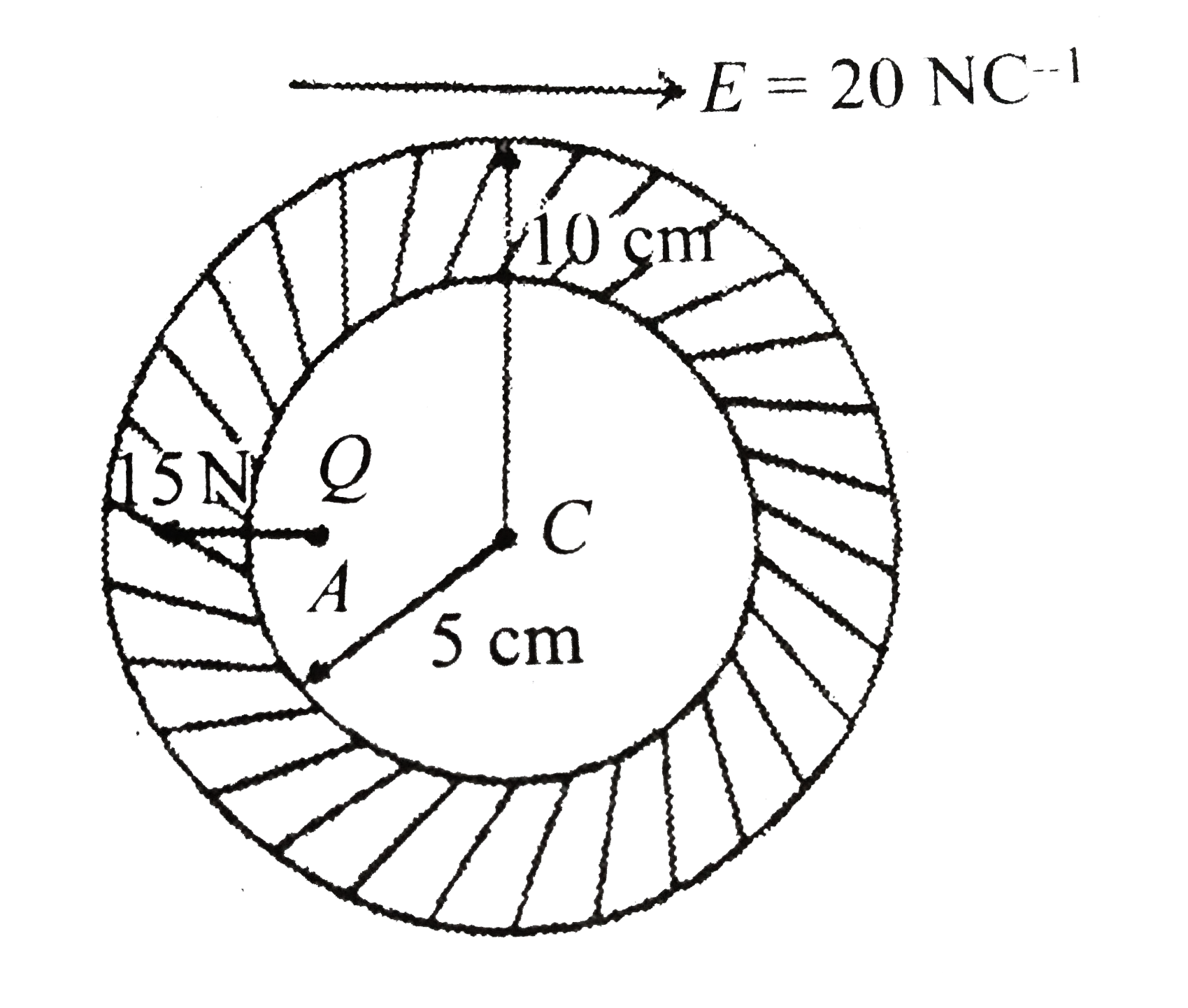
View SolutionTwo conducting spheres of radii r and 2r are placed at very large separation. Each sphere possesses charge Q. These spheres are connected with a conducting wire of resistance R. Then, which of the following is true?
View SolutionTwo concentric spherical conducting shells of radii r and R (r<R) carry charges q and Q respectively . The two shells are now connected by a conducting wire. The final charge on the inner shell is
View SolutionMetallic spheres of radii 6 cm, 8 cm and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
View SolutionMetallic spheres of radii 6 cm, 8 cm and 10 cm respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
View Solution
