A current of 2 mA was passed through an unknown resistor which dissipated a power of 4.4 W. Dissipated power when an ideal power supply of 11 V is connected across it is
11×10−5W
11×10−3W
11×10−4W
11×105W
To solve the problem step by step, we will first determine the resistance of the unknown resistor using the information provided about the current and power. Then, we will calculate the power dissipated when an 11 V power supply is connected across the resistor.
Step 1: Calculate the resistance (R) using the power formula
We know that the power (P) dissipated in a resistor can be expressed in terms of current (I) and resistance (R) as:
P=I2R
Given:
- P=4.4W
- I=2mA=2×10−3A
Substituting the known values into the equation:
4.4=(2×10−3)2R
Calculating (2×10−3)2:
(2×10−3)2=4×10−6
Now substituting this back into the equation:
4.4=4×10−6R
Step 2: Solve for R
To find R, we rearrange the equation:
R=4.44×10−6
Calculating the value:
R=4.44×106=1.1×106Ω
Step 3: Calculate the power dissipated with an 11 V supply
Now we need to calculate the power dissipated when an ideal power supply of 11 V is connected across the resistor. The power can also be expressed in terms of voltage (V) and resistance (R) as:
P=V2R
Given:
- V=11V
- R=1.1×106Ω
Substituting the values into the power formula:
P=1121.1×106
Calculating 112:
112=121
Now substituting this back:
P=1211.1×106
Step 4: Simplify the expression
To simplify:
P=121×10−61.1
Calculating:
P=11×10−5W
Final Answer
Thus, the power dissipated when an ideal power supply of 11 V is connected across the resistor is:
P=1.1×10−4W
---
We know that the power (P) dissipated in a resistor can be expressed in terms of current (I) and resistance (R) as:
P=I2R
- P=4.4W
- I=2mA=2×10−3A
4.4=(2×10−3)2R
(2×10−3)2=4×10−6
4.4=4×10−6R
To find R, we rearrange the equation:
R=4.44×10−6
R=4.44×106=1.1×106Ω
Now we need to calculate the power dissipated when an ideal power supply of 11 V is connected across the resistor. The power can also be expressed in terms of voltage (V) and resistance (R) as:
P=V2R
- V=11V
- R=1.1×106Ω
P=1121.1×106
112=121
P=1211.1×106
To simplify:
P=121×10−61.1
P=11×10−5W
Thus, the power dissipated when an ideal power supply of 11 V is connected across the resistor is:
P=1.1×10−4W
Topper's Solved these Questions
Similar Questions
Knowledge Check
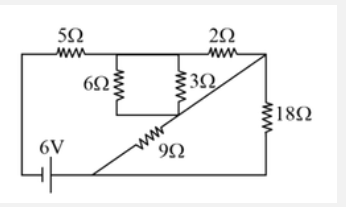
A current of 3A flows through the 2Ω resistor as shown in the circuit. The power dissipated in the 5Ω resistor is
 A5 watt.B4 watt.C2 watt.D1 watt
A5 watt.B4 watt.C2 watt.D1 watt
A current of 2A flows through a 2Ω resistor when connected across a battery. The same battery supplies a current of 0.5A when connected across a 9Ω resistor. The internal resistance of the battery is
View SolutionProve that an ideal capacitor in ac circuit does not dissipate power.
View SolutionIf the power dissipated in 5Ω is 20 W then power dissipated in 4Ω is -

View SolutionThree equal resistors connected in series across a source of emf together dissipate 10W of power. What would be the power dissipated if te same resistors are connected in parallel across the same source of emf?
View SolutionA person with body resistance between his hands of 10KΩ accidentally grasps the terminals of a 18kV power supply.
(i) If the internal resistance of the power supply is 2000Ω, what is the power dissipated in his body?
(ii) What is the power dissipated in his body?
(iii) If the power supply is to be made safe by increasing its internal resistance, what should the internal resistance be for the maximum current in the above situation to be 1.00mA or less?
View SolutionA battery has an open circuit potential difference of 6V between its terminals. When a load resistance of 60Ω is connected across the battery,the total power supplied by the bttery is 0.4W. What should be the load resistance R, so that maximum power will be dissipated in R. Calculated this power. What is the total power supplied by the battery when such a load is connected?
View SolutionWhen a 12V battery is connected across an unknown resistor, there is a current of 2.5mA in the circuit. Find the value of the resistance of the resistor.
View Solution