Two vessels connected by a valve of negligible volume. One container (I) has 2.8 g of N2 at temperature T1(K). The other container (II) is completely evacuated. The container (I) is heated to T2(K)while container (II) is maintained at T2/3(K). volume of vessel (I) is half that of vessel (II). If the valve is opened then what is the mass ratio of N2 is both vessel (WI/WII)?
1:2
1:3
1:6
3:1
The correct Answer is:c
To solve the problem step by step, we will follow these steps:
Step 1: Calculate the number of moles of nitrogen in vessel I.
Given:
- Mass of nitrogen in vessel I, W1=2.8g
- Molar mass of nitrogen, M=28g/mol
Using the formula for moles:
n=WM
n1=2.8g28g/mol=0.1mol
Step 2: Define the volumes of the vessels.
Let:
- Volume of vessel I, V1=V
- Volume of vessel II, V2=2V (since vessel I is half the volume of vessel II)
Step 3: Write the ideal gas equations for both vessels.
For vessel I:
P1V1=n1RT1(before opening the valve)
After the valve is opened, the number of moles in vessel I will be n1−x:
P1V1=(0.1−x)RT2
For vessel II:
P_2 V_2 = n_2 R T_2/3 \quad \text{(where n_2 = x )}
P2(2V)=xRT23
Step 4: Relate the pressures in both vessels.
From the ideal gas law, we can express the pressures:
P1=(0.1−x)RT2V
P2=xRT232V
Step 5: Set the pressures equal after the valve is opened.
Since the pressure will equalize when the valve is opened:
(0.1−x)RT2V=xRT232V
Step 6: Cancel out common terms and solve for x.
Cancel R and T2 from both sides:
(0.1−x)=x6
Multiply through by 6:
6(0.1−x)=x
0.6−6x=x
Combine like terms:
0.6=7x
x=0.67≈0.0857mol
Step 7: Calculate the mass of nitrogen in vessel II.
Using the number of moles transferred to vessel II:
W2=x×M=0.67×28≈2.4g
Step 8: Calculate the mass of nitrogen remaining in vessel I.
The remaining moles in vessel I:
n1−x=0.1−0.67=0.1×7−0.67=0.7−0.67=0.17
Calculating the mass:
W1=(0.17)×28≈0.4g
Step 9: Calculate the mass ratio W1W2.
W1W2=0.4g2.4g=16
Final Answer:
The mass ratio of N2 in both vessels W1W2 is 16.
---
Given:
- Mass of nitrogen in vessel I, W1=2.8g
- Molar mass of nitrogen, M=28g/mol
n=WM
n1=2.8g28g/mol=0.1mol
Let:
- Volume of vessel I, V1=V
- Volume of vessel II, V2=2V (since vessel I is half the volume of vessel II)
For vessel I:
P1V1=n1RT1(before opening the valve)
After the valve is opened, the number of moles in vessel I will be n1−x:
P1V1=(0.1−x)RT2
P_2 V_2 = n_2 R T_2/3 \quad \text{(where n_2 = x )}
P2(2V)=xRT23
From the ideal gas law, we can express the pressures:
P1=(0.1−x)RT2V
P2=xRT232V
Since the pressure will equalize when the valve is opened:
(0.1−x)RT2V=xRT232V
Cancel R and T2 from both sides:
(0.1−x)=x6
Multiply through by 6:
6(0.1−x)=x
0.6−6x=x
Combine like terms:
0.6=7x
x=0.67≈0.0857mol
Using the number of moles transferred to vessel II:
W2=x×M=0.67×28≈2.4g
The remaining moles in vessel I:
n1−x=0.1−0.67=0.1×7−0.67=0.7−0.67=0.17
Calculating the mass:
W1=(0.17)×28≈0.4g
W1W2=0.4g2.4g=16
The mass ratio of N2 in both vessels W1W2 is 16.
Topper's Solved these Questions
- GASEOUS STATEBook:NARENDRA AWASTHI ENGLISHChapter:GASEOUS STATEExercise:Level 3 Passage 1
Explore 4 Videos
- GASEOUS STATEBook:NARENDRA AWASTHI ENGLISHChapter:GASEOUS STATEExercise:Level 3 Passage 2
Explore 6 Videos
- GASEOUS STATEBook:NARENDRA AWASTHI ENGLISHChapter:GASEOUS STATEExercise:Subjective problems
Explore 15 Videos
- ELECTROCHEMISTRYBook:NARENDRA AWASTHI ENGLISHChapter:ELECTROCHEMISTRYExercise:Subjective problems
Explore 14 Videos
- IONIC EEQUILIBRIUMBook:NARENDRA AWASTHI ENGLISHChapter:IONIC EEQUILIBRIUMExercise:Subjective problems
Explore 1 Video
Similar Questions
Two vessels are connected by a valve of negligible volume. One container, A has 2.8 g N2 at T1K. The other container, B is completely evacuated. The container A is heated to T2K, while container B is maintained at T23K . Volume of A is half that of B. If the valve is opened, then
View SolutionA vessel contains 1.60g of oxygen and 2.80g of nitrogen. The temperature is maintained at 300K and the voume of the vessel is 0.166m3. Find the pressure of the mixture.
View Solution
Knowledge Check
A monatomic gas on n molecules is heated from temperature T1 to T2 under two different conditions (i) constant volume, (ii) constant pressure. The change of internal energy of the gas
Amore of (i)Bmore of (ii)Csame in both casesDindependent of number of moles
Two closed vessels of equal volume containing air at pressure P1 and temperature T1 are connected to each other through a narrow tube. If the temperature in one of the vessels is now maintained at T1 and that in the other at T2, what will be the pressure in the vessels?
View SolutionTwo closed vessels of equal volume containing air at pressure P1 and temperature T1 are connected to each other through a narrow tube. If the temperature in one of the vessels is now maintained at T1 and that in the other at T2, what will be the pressure in the vessels?
View SolutionA vessel contains 28g of N2 and 32g of O2 at temperature T=1800K and pressure 2atm. What would be the pressure when N2 dissociates 30% and O2 dissociates 50% and temperature remains constant ?
View SolutionTwo closed vessel A and B of equal volume containing air at pressure P1 and temperature T1 are connected to each other through a naroow open tube. If th temperature of one is now maintained at T1 and other at T2 (wehre T1>T2 ) then that what will be the final pressure ?
View SolutionEqual masses of air are sealed in two vessels, one if volume V0and the other of volume 2V0.If the first vessel is maintained at a temperature 300K and the other at 600K, find the ratio of the pressures in the two vessels.
View Solution2g of hydrogen is sealed in a vessel of volume 0.02m3and is maintained at 300K. Calculate the pressure in the vessel.
View SolutionTwo closed bulbs of equal volume (V) containing an ideal gas initially at pressure Pi and temperature T1 are connected through a narrow tube of negligible volume as shown in the figure below . The temperature of one of the bulbs is then raised to T2 . the final pressure Pf is
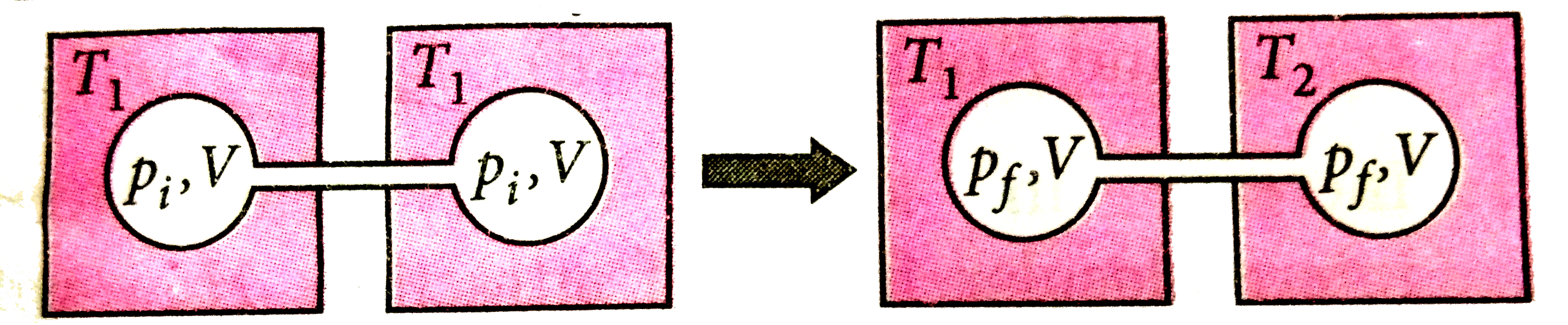
View Solution

