A long vertical wire carrying a current of 10A in the upward direction is placed in a region where a horizontal magnetic field of magnitude(2.0×10−3) T exists from south to north. Find the point where the resultant magnetic field is zero.
To solve the problem of finding the point where the resultant magnetic field is zero, we can follow these steps:
Step 1: Understand the Setup
We have a long vertical wire carrying a current of 10 A in the upward direction. There is also a horizontal magnetic field of magnitude BH=2.0×10−3T directed from south to north.
Step 2: Determine the Direction of the Magnetic Fields
Using the right-hand rule, we can determine the direction of the magnetic field created by the current in the wire. If the current is flowing upward, the magnetic field around the wire will circulate in a counter-clockwise direction when viewed from above.
Step 3: Identify the Points of Interest
We need to find a point where the magnetic field due to the wire (B) cancels out the horizontal magnetic field (BH). This point can be either to the east or west of the wire.
Step 4: Write the Expression for the Magnetic Field Due to the Wire
The magnetic field (B) at a distance X from a long straight wire carrying current I is given by the formula:
B=μ0I2πX
where μ0=4π×10−7T m/A.
Step 5: Set Up the Equation for Zero Resultant Magnetic Field
At the point where the resultant magnetic field is zero, the magnetic field due to the wire must equal the horizontal magnetic field:
BH=B
Substituting the expressions we have:
2.0×10−3=μ0I2πX
Step 6: Substitute Known Values
Substituting μ0=4π×10−7T m/A and I=10A:
2.0×10−3=(4π×10−7)×102πX
Step 7: Simplify the Equation
The π terms cancel out:
2.0×10−3=4×10−62X
This simplifies to:
2.0×10−3=2×10−6X
Step 8: Solve for X
Rearranging gives:
X=2×10−62.0×10−3=2×10−62×10−3=10−3m
Conclusion
The point where the resultant magnetic field is zero is at a distance of X=10−3m (or 1 mm) from the wire.
---
We have a long vertical wire carrying a current of 10 A in the upward direction. There is also a horizontal magnetic field of magnitude BH=2.0×10−3T directed from south to north.
Using the right-hand rule, we can determine the direction of the magnetic field created by the current in the wire. If the current is flowing upward, the magnetic field around the wire will circulate in a counter-clockwise direction when viewed from above.
We need to find a point where the magnetic field due to the wire (B) cancels out the horizontal magnetic field (BH). This point can be either to the east or west of the wire.
The magnetic field (B) at a distance X from a long straight wire carrying current I is given by the formula:
B=μ0I2πX
where μ0=4π×10−7T m/A.
At the point where the resultant magnetic field is zero, the magnetic field due to the wire must equal the horizontal magnetic field:
BH=B
Substituting the expressions we have:
2.0×10−3=μ0I2πX
Substituting μ0=4π×10−7T m/A and I=10A:
2.0×10−3=(4π×10−7)×102πX
The π terms cancel out:
2.0×10−3=4×10−62X
This simplifies to:
2.0×10−3=2×10−6X
Rearranging gives:
X=2×10−62.0×10−3=2×10−62×10−3=10−3m
The point where the resultant magnetic field is zero is at a distance of X=10−3m (or 1 mm) from the wire.
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer
6 Videos
Similar Questions
A long, vertical straight wire carrying a current of 30 A is placed in an external, uniform magnetic field of (4.0×(10−4) T exists from south to north. Find magnetic field at a point 2.0 away from the wire.
View SolutionA long, straight wire carrying a current of 1.0 A is placed horizontally in a uniform magnetic field B= (1.0×10−5) T pointing vertically upward. Find the magnitude of the resultant magnetic field at the points P and Q, both situated at a distance of 2.0 cm from the wire in the same horizontal plane.
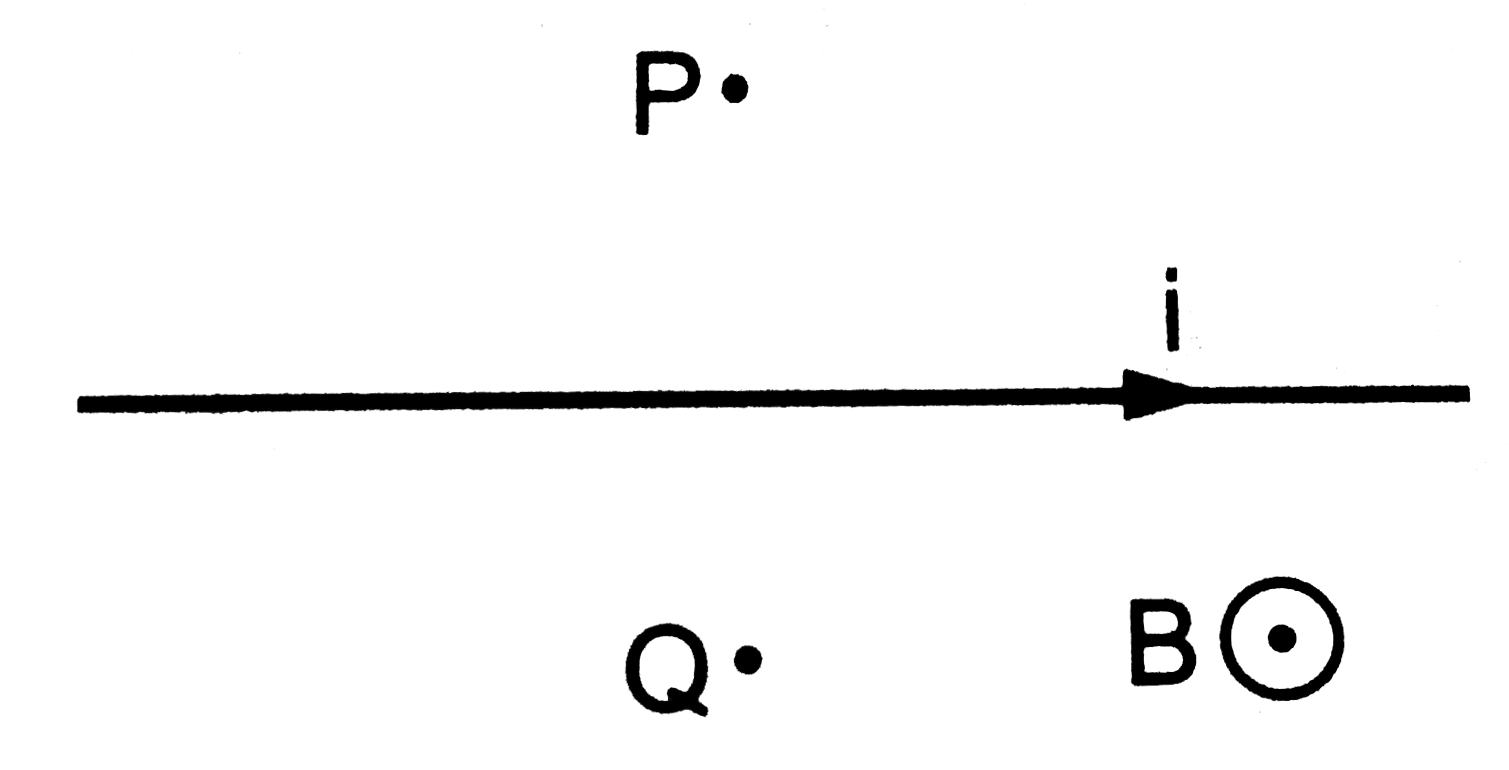
View Solution
Knowledge Check
An 8 cm long wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. If the magnetic field inside the solenoid is 0.3 T, then magnetic force on the wire is
A0.14NB0.24NC0.34ND0.44N
A long straight wire carrying current of 30A is placed in an external uniform magnetic field of induction 4×10−4T. The magnetic field is acting parallel to the direction of current. The magnitude of the resultant magnetic induction in tesla at a point 2.0cm away from the wire is
View SolutionA long straight wire carrying current of 30A is placed in an external unifrom magnetic field of induction 4×104T. The magnetic field is acting parallel to the direction of current. The maggnetic of the resultant magnetic inuduction in tesla at a point 2.0cm away form the wire is
View SolutionAn alpha particle is projected vertically upward a speed of 3.0X104kms−1 in a region where a magnetic field of magnitude 1.0 T exists in the direction south to north. Find the magnetic force that acts on the a particle.
View SolutionThe horizontal component of the earth's magnetic field is 3.6×10−5T where the dip is 60∘. Find the magnitude of the earth's magnetic field.
View SolutionTwo very long, straight wires carrying, currents as shown in Fig. Find all locations where the net magnetic field is zero.

View SolutionTwo parallel wires carry equal currents of 10A along the same direction and are separated by a distance of 2.0 cm. Find the magnetic field at a point which is 2.0 cm away from each of these wires.
View SolutionA long cylindrical wire carrying current of 10A has radius of 5mm find its its magnetic field induction at a point 2mm from the centre of the wire
View Solution
