A particle goes in a circle of radius 2.0 cm. A concave mirror of focal length 20 cm is placed with its principal axis passing through the centre of the circle and perpendicular to its plane. The distance between the pole of the mirror and the centre of the circle is 30 cm. Calculate the radius of the circle formed by the image.
The correct Answer is:C, D
To solve the problem, we will follow these steps:
Step 1: Understand the Setup
We have a concave mirror with a focal length of f=−20cm (the negative sign indicates that it is a concave mirror). The distance from the mirror to the center of the circle (the object) is u=−30cm (the negative sign indicates that the object is in front of the mirror).
Step 2: Use the Mirror Formula
The mirror formula is given by:
1f=1v+1u
Where:
- f is the focal length,
- v is the image distance,
- u is the object distance.
Substituting the known values into the formula:
1−20=1v+1−30
Step 3: Solve for v
Rearranging the equation:
1v=1−20+130
Finding a common denominator (which is 60):
1v=−360+260=−160
Thus,
v=−60cm
Step 4: Calculate Magnification
The magnification m is given by:
m=−vu
Substituting the values:
m=−−60−30=2
Step 5: Calculate the Height of the Image
The height of the object is given as h0=2cm. The height of the image hi can be calculated using:
hi=m⋅h0
Substituting the values:
hi=2⋅2=4cm
Step 6: Determine the Radius of the Circle Formed by the Image
Since the image is formed at a distance of v=−60cm and the height of the image is 4cm, the radius of the circle formed by the image is equal to the height of the image, which is:
Radius of the circle formed by the image=4cm
Final Answer
The radius of the circle formed by the image is 4cm.
---
We have a concave mirror with a focal length of f=−20cm (the negative sign indicates that it is a concave mirror). The distance from the mirror to the center of the circle (the object) is u=−30cm (the negative sign indicates that the object is in front of the mirror).
The mirror formula is given by:
1f=1v+1u
Where:
- f is the focal length,
- v is the image distance,
- u is the object distance.
1−20=1v+1−30
Rearranging the equation:
1v=1−20+130
Finding a common denominator (which is 60):
1v=−360+260=−160
Thus,
v=−60cm
The magnification m is given by:
m=−vu
Substituting the values:
m=−−60−30=2
The height of the object is given as h0=2cm. The height of the image hi can be calculated using:
hi=m⋅h0
Substituting the values:
hi=2⋅2=4cm
Since the image is formed at a distance of v=−60cm and the height of the image is 4cm, the radius of the circle formed by the image is equal to the height of the image, which is:
Radius of the circle formed by the image=4cm
The radius of the circle formed by the image is 4cm.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:HC VERMA ENGLISHChapter:GEOMETRICAL OPTICSExercise:EXAMPLE
Explore 9 Videos
- GEOMETRICAL OPTICSBook:HC VERMA ENGLISHChapter:GEOMETRICAL OPTICSExercise:Question For short Answer
Explore 18 Videos
- GEOMETRICAL OPTICSBook:HC VERMA ENGLISHChapter:GEOMETRICAL OPTICSExercise:Objective -2
Explore 7 Videos
- GAUSS LAWBook:HC VERMA ENGLISHChapter:GAUSS LAWExercise:Short Question
Explore 7 Videos
- LIGHT WAVESBook:HC VERMA ENGLISHChapter:LIGHT WAVESExercise:Question for short Answer
Explore 11 Videos
Similar Questions
Knowledge Check
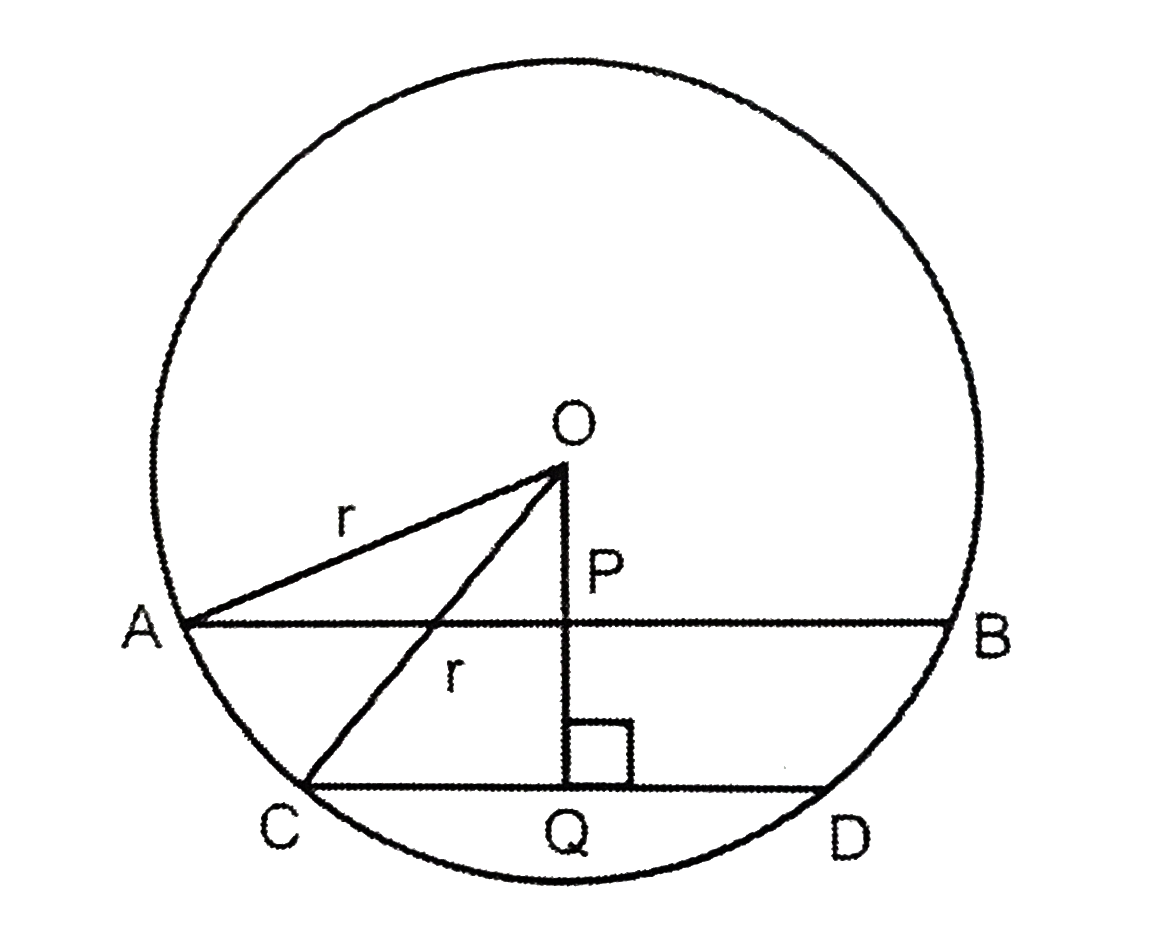
2 parallel chords 24 cm, and 18 cm, are on the same side of the centre of a circle. If the distance between the chords is 3 cm, calculate the radius of the circle.A15 cmB14 cmC13 cmD12 cm
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4cm. Find the radius of the circle.
View SolutionAn arc of length 20π cm subtends an angle of 144o at the centre of a circle. Find the radius of the circle.
View SolutionThe length of the tangent from a point A to a circle, of radius 3cm, is 4cm. The distance of A from the centre of the circle is
View SolutionFind the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
View SolutionAn object is placed at a distance of 20 cm from a concave mirror of focal lenght 10 cm. What is the image distance?
View SolutionA chord of length 6 cm is drawn in a circle of radius 5 cm. Calculate its distance from the centre of the circle.
View Solution

