Two strings A and B made of same material are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed vA and on B with speed vB. The ratio vAvB is
12
2
14
4
The correct Answer is:A
To solve the problem, we need to find the ratio of the speeds of transverse waves on two strings A and B, given that they are made of the same material and stretched by the same tension, but have different radii.
1. Understanding Wave Speed in Strings:
The speed of a transverse wave on a string is given by the formula:
v=√Tμ
where T is the tension in the string and μ is the linear mass density of the string.
2. Linear Mass Density:
The linear mass density μ is defined as:
μ=mL
where m is the mass of the string and L is its length. For a string of uniform cross-section, we can also express μ in terms of the volume and the area of cross-section:
μ=ρ⋅AL
where ρ is the density of the material and A is the cross-sectional area of the string.
3. Cross-sectional Area:
The cross-sectional area A of a cylindrical string can be calculated using the radius r:
A=πr2
4. Comparing the Two Strings:
Let the radius of string B be r. Then, the radius of string A is given as double that of string B:
rA=2r
Therefore, the cross-sectional areas for the two strings are:
AA=π(2r)2=4πr2
AB=πr2
5. Calculating Linear Mass Densities:
Now we can express the linear mass densities for both strings:
μA=ρ⋅AAL=ρ⋅4πr2L
μB=ρ⋅ABL=ρ⋅πr2L
6. Finding the Speeds:
Since the tension T is the same for both strings, we can write the speeds as:
vA=√TμA=
⎷Tρ⋅4πr2L=√TLρ⋅4πr2
vB=√TμB=
⎷Tρ⋅πr2L=√TLρ⋅πr2
7. Finding the Ratio of Speeds:
Now, we can find the ratio vAvB:
vAvB=√TLρ⋅4πr2√TLρ⋅πr2=√1/4√1=12
8. Final Result:
Therefore, the ratio of the speeds of the waves on strings A and B is:
vAvB=12
The speed of a transverse wave on a string is given by the formula:
v=√Tμ
where T is the tension in the string and μ is the linear mass density of the string.
The linear mass density μ is defined as:
μ=mL
where m is the mass of the string and L is its length. For a string of uniform cross-section, we can also express μ in terms of the volume and the area of cross-section:
μ=ρ⋅AL
where ρ is the density of the material and A is the cross-sectional area of the string.
The cross-sectional area A of a cylindrical string can be calculated using the radius r:
A=πr2
Let the radius of string B be r. Then, the radius of string A is given as double that of string B:
rA=2r
Therefore, the cross-sectional areas for the two strings are:
AA=π(2r)2=4πr2
AB=πr2
Now we can express the linear mass densities for both strings:
μA=ρ⋅AAL=ρ⋅4πr2L
μB=ρ⋅ABL=ρ⋅πr2L
Since the tension T is the same for both strings, we can write the speeds as:
vA=√TμA=
⎷Tρ⋅4πr2L=√TLρ⋅4πr2
vB=√TμB=
⎷Tρ⋅πr2L=√TLρ⋅πr2
Now, we can find the ratio vAvB:
vAvB=√TLρ⋅4πr2√TLρ⋅πr2=√1/4√1=12
Therefore, the ratio of the speeds of the waves on strings A and B is:
vAvB=12
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Objective -29videos
WAVE MOTION AND WAVES ON A STRING
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Exercises57videos
WAVE MOTION AND WAVES ON A STRING
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Worked out Examples10videos
WAVE MOTION AND WAVES ON A STRING
- BOOK - HC VERMA ENGLISHCHAPTER - THE FORCESEXERCISE - Questions for short Answer9videos
THE FORCES
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer16videos
WORK AND ENERGY
Similar Questions
Two strings of same material are stretched to the same tension . If their radii are in the ratio 1:2 , then respective wave velocities in them will be in ratio
View Solutionboth the strings , shown in figure are made of same material and have same cross - section. The pulleys are light the wave speed pf a travsverse wave in the string AB is v1 and in CD is v2. The ratio v1/v2 is
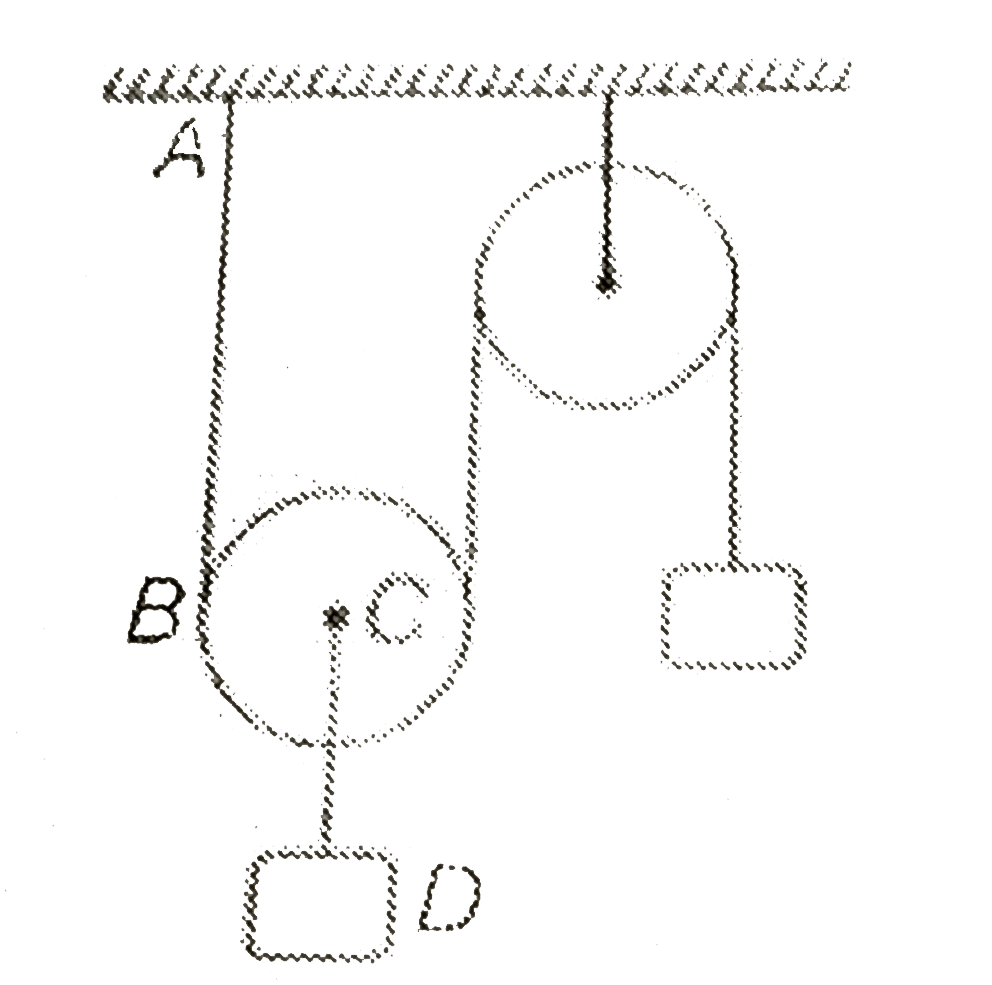 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two planets A and B have the same material density. If the radius of A is twice that of B, then the ratio of the escape velocity VA/VB is
A2B√2C1/√2D1/2
Two strings of copper are stretched to the same tension. If their cross-section area are in the ratio 1 : 4 , then the respective wave velocities will be
View SolutionBoth the strings, shown in figure, are made of same material and have same cross-section. The pulleys are light. The wave speed of transverse wave in the string AB is v1 and in CD it is v2, the v1/v2 is
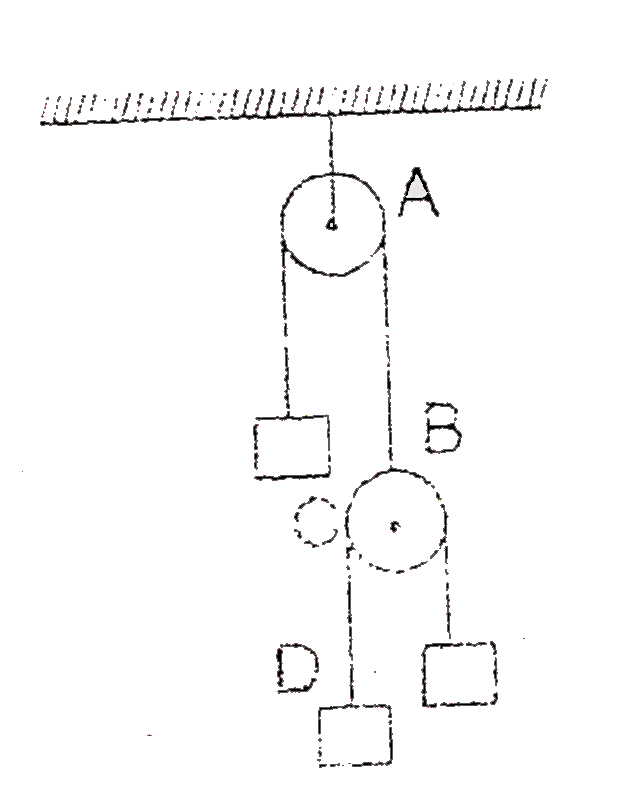 View Solution
View SolutionTwo uniform strings AandB made of steel are made to vibrate under the same tension. If the first overtone of A is equal to the second overtone of B and if the radius of A is twice that of B, the ratio of the lengths of the strings is
View SolutionTwo vibrating strings of the same material but lengths L and 2L have radii 2r and r respectively. They are stretched under the same tension. Both the string vibrate in their fundamental nodes, the one of length L with freuqency v1 and the other with frequency v2. the ratio v1/v2 is given by
View SolutionTwo stretched wires A and B of same material vibrate independently. If the tension, length and radius of wire B is half those of wire A, then ratio of fundamental frequency of vibration of A and B is
View SolutionTwo bars A and B of circular cross section, same volume and made of the same material, are subjected to tension. If the diameter of A is half that of B and if the force applied to both the rod is the same and it is in the elastic limit, the ratio of extension of A to that of B will be
View SolutionTwo strings A and B, made of the same material, have equal lengths. The cross sectional area of A is half that of B while the tension on A is twice that on B. The ratio of the velocities of transverse waves in A and B is
View Solution
