A light wire AB of length 10 cm can slide on a vertical frame as shown in figure. There is a film of soap solution trapped between the frame and the wire. Find the load W that should be suspended from the wire to keep it in equilibrium. Neglect friction. Surface tension of soat solution =25 dyne cm−1. Take g=10ms−2
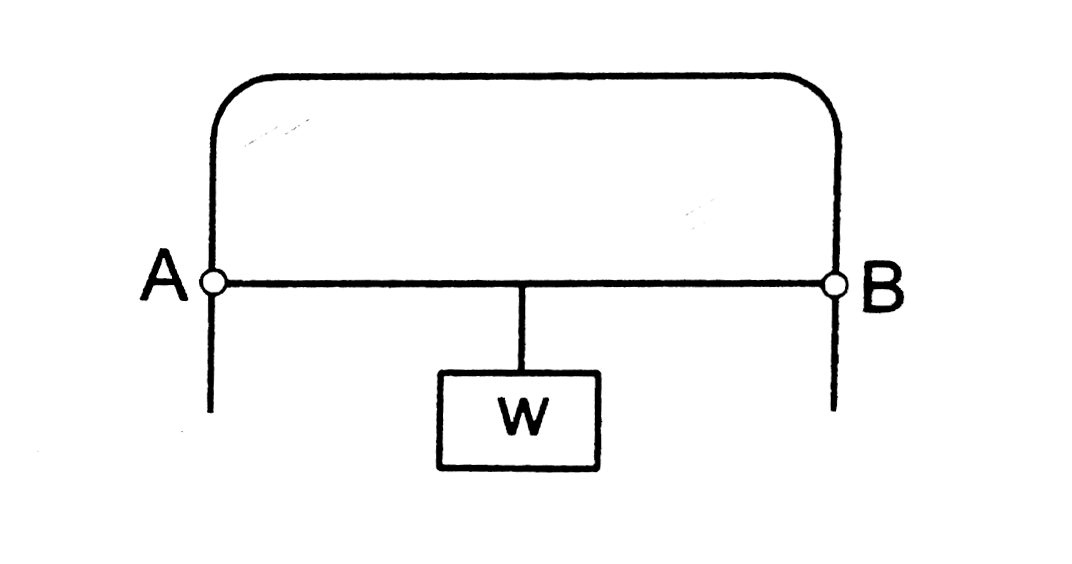
Soap solutioin film will be formed on both sides of the frame. Each film is in contact with the wire along a distanc eo 10 cm The force exerted by the film on the wire
=2×(10cm)×(25dy≠cm−1)
=500dy≠=5×10−3N.
This force acts vertically upward and should be balanced by the load. Hence the load that should be suspended is 5×10−3N. The mass of the load should be
5×106−3N10ms−2=5×10−4kg=0.54g.
Topper's Solved these Questions
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Question For short Anser
18 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
- SOUND WAVESBOOK - HC VERMA ENGLISHCHAPTER - SOUND WAVESEXERCISE - All Questions
133 Videos
Similar Questions
A film of soap solution is trapped between a vertical frame and a light wire ab of length 0.1 m. If g=10m/s2 , then the load mass that should be suspended from the wire to keep it in equilibrium is : (σ=25×10−3N/m)
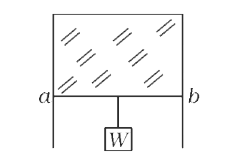
View Solution_E01_194_Q01.png)
PQRS is a rectangular frame of copper wire shown in figure the side RS of the frame is movable. If a soap film is formed on it then what is the diameter of the wire to maintain equilibirum (given surface tension of soap solution =0.045N/m and density of copper =8.96×103kg/m3)
View SolutionA 10 cm long wire is placed horizontal on the surface of water and is gently pulled up with a force of 2×10−2 N to keep the wire in equilibrium. The surface tension, in Nm−1 of water is
View SolutionA wire of mass 1g is kept horizontally on the surface of water. The length of the wire that does not break the surface film is (surface tension of water is 70dy≠cm−1)
View SolutionA film of soap solution is formed on a loop frame loop of 6.28cm long thread is gently put on the film and the film is broken with a needle inside the loop. The tread loop takes the shape of a circle. Find the tension in the thread. Surface tension of soap solution =0.030n/m.
View SolutionA 50 cm long wire of mass 20 g suports a mass of 1.6kg as shown in figure. Find the fundamental frequency of the portioin of the strig between the wall and the pulley. Take g=10ms−2.

View SolutionHow much work will be done in increasing the diameter of a soap bubble from 2 cm to 5 cm. Surface tension of soap solution is 3.0×10−2Nm−1.
View SolutionConsider a U-shaped frame with a sliding wire of length l and mass 'm' on its arm. It is dipped in a soap solution, taken out and placed in vertical position as shown in figure. Choose minimum value of m so that does not descent (Surface tension of soap solution is S)

View SolutionA wire forming a loop is dipped into soap solution and taken out so that a film of soap solution is formed. A loop of 6.28 cm long thread is gently put on the film and the film is pricked with a needle inside the loop. The thread loop takes the shape of a circle. Find the tension in the thread. Surface tension of soap solution =0.030Nm−1.
View SolutionA wire forming a loop is dipped into soap solution and taken out so that a film of soap solution is formed. A loop of 6.28 cm long thread is gently put on the film and the film is pricked with a needle inside the loop. The thread loop takes the shape of a circle. Find the tension in the thread. Surface tension of soap solution =0.030Nm−1.
View Solution
