A particle of mass 0.50 kg executes a simple harmonic motion under a force F=−(50Nm−1)x. If it crosses the centre of oscillation with a speed of 10ms−1, find the amplitude of the motion.
To solve the problem, we will use the principles of energy conservation in simple harmonic motion (SHM). The total mechanical energy in SHM is conserved and can be expressed in terms of kinetic energy and potential energy.
1. Identify the Given Values:
- Mass of the particle, m=0.50kg
- Speed at the center of oscillation, v=10m/s
- Force constant (spring constant), k=50N/m
2. Understand Energy at the Center of Oscillation:
At the center of oscillation (equilibrium position), the kinetic energy (KE) is maximum, and the potential energy (PE) is zero. The total mechanical energy (E) at this point can be expressed as:
E=KE=12mv2
3. Calculate the Kinetic Energy:
Substitute the values into the kinetic energy formula:
KE=12×0.50kg×(10m/s)2
KE=12×0.50×100=25J
4. Relate Kinetic Energy to Potential Energy:
At maximum displacement (amplitude A), the kinetic energy is zero, and the potential energy is maximum. The potential energy can be expressed as:
PE=12kA2
Since energy is conserved:
KE=PE⇒25J=12kA2
5. Substitute the Spring Constant:
Substitute k=50N/m into the equation:
25=12×50×A2
6. Solve for Amplitude A:
25=25A2
Divide both sides by 25:
1=A2
Taking the square root:
A=1m
Final Answer:
The amplitude of the motion is A=1m.
---
- Mass of the particle, m=0.50kg
- Speed at the center of oscillation, v=10m/s
- Force constant (spring constant), k=50N/m
At the center of oscillation (equilibrium position), the kinetic energy (KE) is maximum, and the potential energy (PE) is zero. The total mechanical energy (E) at this point can be expressed as:
E=KE=12mv2
Substitute the values into the kinetic energy formula:
KE=12×0.50kg×(10m/s)2
KE=12×0.50×100=25J
At maximum displacement (amplitude A), the kinetic energy is zero, and the potential energy is maximum. The potential energy can be expressed as:
PE=12kA2
Since energy is conserved:
KE=PE⇒25J=12kA2
Substitute k=50N/m into the equation:
25=12×50×A2
25=25A2
Divide both sides by 25:
1=A2
Taking the square root:
A=1m
The amplitude of the motion is A=1m.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:HC VERMA ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:worked out Examples
Explore 22 Videos
- SIMPLE HARMONIC MOTIONBook:HC VERMA ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Objective -1
Explore 21 Videos
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Questions for short Answer
Explore 21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBook:HC VERMA ENGLISHChapter:SOME MECHANICAL PROPERTIES OF MATTERExercise:Objective-2
Explore 7 Videos
Similar Questions
A particle of mass 0.1 kg executes SHM under a for F=(−10x) N. Speed of particle at mean position 6m/s. Then amplitude of oscillations is
View SolutionA particle of mass 40 g executes a simple harmonic motion of amplitude 2.0 cm. If the time period is 0.20 s, find the total mechanical energy of the system.
View SolutionA particle of mass 40 g executes a simple harmonic motion of amplitude 2.0 cm. If the time period is 0.20 s, find the total mechanical energy of the system.
View SolutionA particle executes simple harmonic motion of period 16s. Two seconds later after it passes through the center of oscillation its velocity is found to be 2m/s. Find the amplitude.
View SolutionA paricle of mass 30kg executes a simple harmonic motion. The restorting force is provided by a spring of spring constant 80N/m. Find the time period.
View SolutionA particle of mass 200g executes a simple harmonic motion. The restoring force is provided by a spring of spring constant 80N/m. Find the time period.
View SolutionA partical of mass 0.2kg executes simple harmonic motion along a path of length 0.2m at the rate of 600oscillations per minute. Assum at t=0. The partical start SHM in positive direction. Find the kinetic potential energies in joules when the displacement is x=A/2 where, A stands for the amplitude.
View SolutionA body of mass 0.01 kg executes simple harmonic motion about x = 0 under the influence of a force as shown in figure. The time period of SHM is
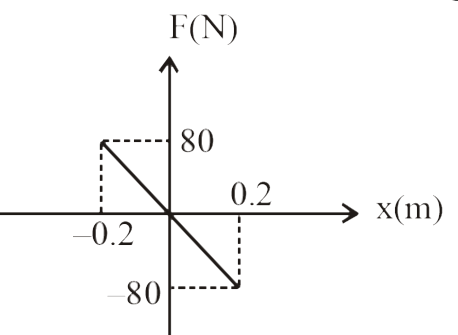
View SolutionA body of mass 0.01 kg executes simple harmonic motion (SHM) about x=0 under the influence of a force shown in the figure. The period of the SHM is
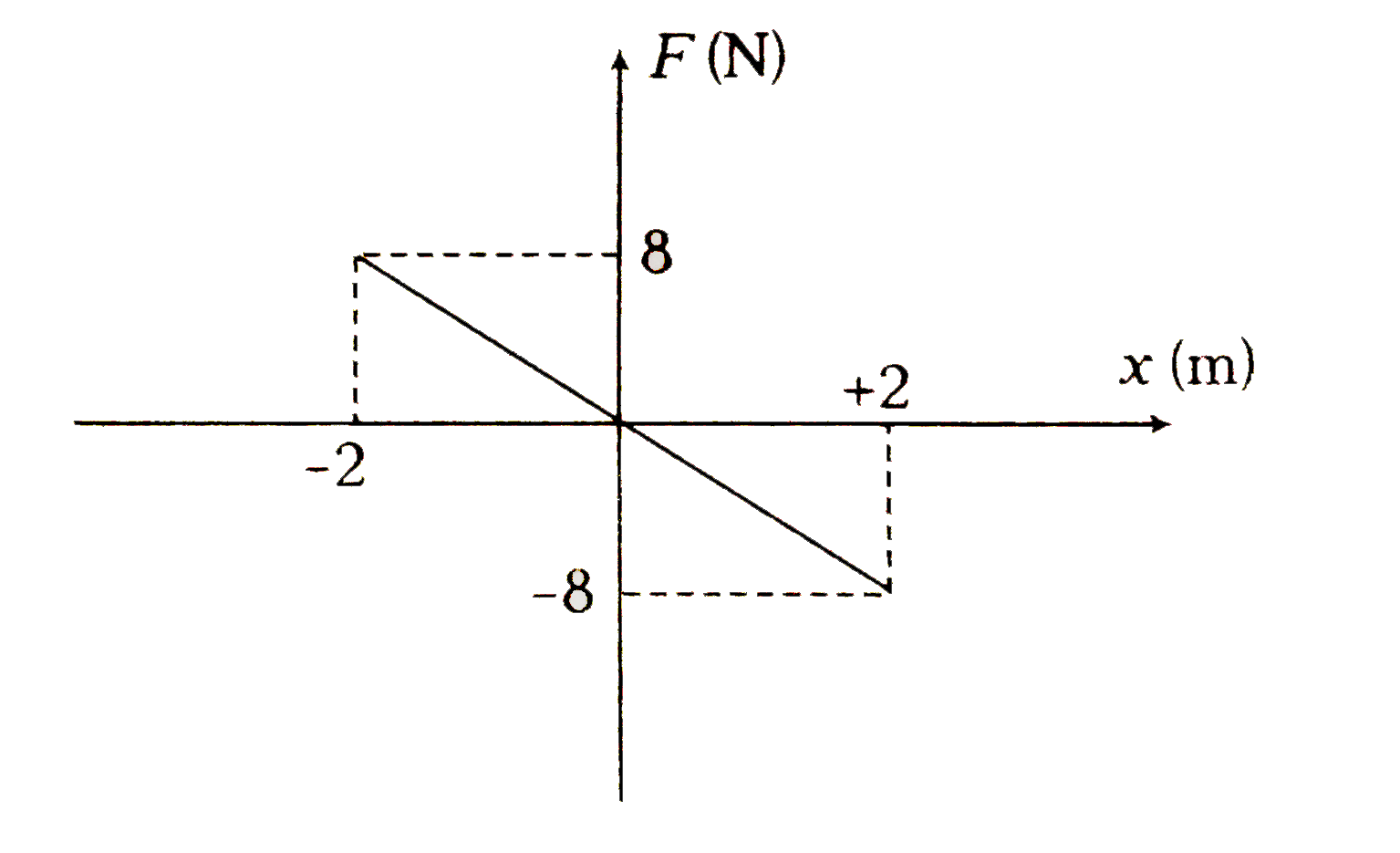
View SolutionA particle executing simple harmonic motion of amplitude 5cm has maximum speed of 31.4cm/s. The frequency of its oscillation is
View Solution