Particles of masses 1g, 2g, 3g ….100g are kept at the marks 1cm, 2cm, 3cm …., 100 cm respectively on a metre scale. Find the moment of inertia of the system of particles about a perpendicular bisector of the metre scale.
The correct Answer is:B, C, D
Masses of 1gm, 2gm …………100 gm are kept at themarks 1cm, 2cm…………..100 cm on the xis resectively. A perpendicular axis is passed at the 50th particle.
Therefore on the L.H.S. of the axis there will be 49 particles and on the R.H.S there are 50 particles.
Consider the two particles at the position 49 cm and 51 cm.
Moment of inertia due to these two particles will be:
=49×(1)2+51×(1)2
=100×1=100gm−cm2
similarly if we consider 48th and 52nd term we will get 100×(2)2gm−cm2.
Threfore we wil get 49 such set and one lone particle at 100 cm. Threfoee totl moment of inertia
=100(12+22+32+........+492)+100(50)2
=100(1^2+2^2+3^2+..........+50^2)<br>=100xx(50xx51xx101)/6<br>=100x25xx17xx101<br>=100xx101xx425<br>=4292500gm-cm^2<br>=429kg-m^2=0.43kg-m^2
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer21videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -214videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer13videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer15videos
SIMPLE HARMONIC MOTION
Similar Questions
Two masses of 3kg and 5kg are placed at 20 cm and 70cm marks respectively on a light wooden meter scale. The M.I. of the system about an axis passign through 100cm mark and perpendicular to the meter scale is
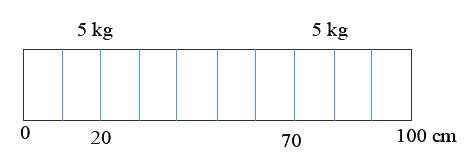 View Solution
View SolutionThree particles, each of mass 200 g are kept at the corners of an equilateral triangle of side 10 cm. Find the moment of inertia of the system about an axis
a. joining two of the particles
b. passing through one of the particle perpendicular to the plane of the particles.View Solution
Knowledge Check
- Question 1 - Select One
If the centre of gravity of a metre scale of mass 80g lies at the 45 cm mark, then which one of the following diagrams will show the balanced position of the scale.
A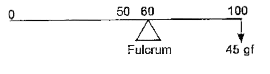 B
B C
C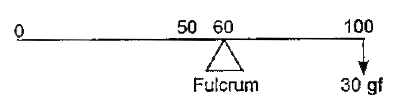 D
D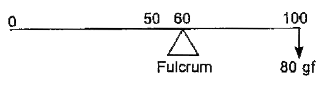
Three particles of masses 1 g, 2g and 3 g are kept at points (2cm,0), (0.6 cm), (4cm, 3cm) find moment of inertia of all three particles (in gm−cm(2)) about (a) x-axis
(b). Y-axis
(c). Z-axis.View SolutionThe coordinates of the centre of mass of a system of three particles of mass 1g,2g and 3g are (2,2,2). Where should a fourth particle of mass 4 g be positioned so that the centre of mass of the four particle system is at the origin of the three-dimensional coordinate system ?
View SolutionA particle of mass 100 g is kept on the surface of a uniform sphere of mass 10 kg and radius 10 cm. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
View SolutionTwo discs of same mass and same thickness have densities as 17g/cm3 and 51g/cm3. The ratio of their moment of inertia about their central axes is
View SolutionA uniform metre scale can be balanced at the 70.0 cm mark when a mass of 0.05 kg is hung from the 94.0 cm mark.
Find the mass of the metre scale.View SolutionTwo immiscible of densities 2.5g/cm3 and 0.8g/cm3 are taken in the ratio of their masses as 2:3 respectively find the average density of the liquid conbination.
View SolutionA cork has a volume 25cm3 . The density of cork is 0.25gcm−3 . Find the mass of the cork.
View Solution
