A block of mass m and a pan of equal mass are connected by a string going over a smooth light pulley as shown in figure. Initially the system is at rest when a particle of mass m falls on the pan and sticks to it. If the particle strikes the pan with a speed v find the speed with which the system moves just after the collision.
To solve the problem step by step, we will use the principles of conservation of momentum and the concept of impulsive forces.
Step 1: Understand the system
We have:
- A block of mass m hanging on one side of a pulley.
- A pan of mass m on the other side.
- A particle of mass m falling onto the pan with an initial speed v.
Step 2: Define the direction of motion
We will take the downward direction as positive. Therefore:
- The velocity of the falling particle just before impact is +v.
- The initial velocity of the pan and block is 0.
Step 3: Analyze the collision
When the particle strikes the pan and sticks to it, we need to consider the change in momentum due to the collision.
Step 4: Write the momentum conservation equation
Before the collision, the momentum of the system is only due to the falling particle:
Initial momentum=mv
After the collision, the combined mass (particle + pan) moves together with some velocity u:
Final momentum=(m+m)u=2mu
Step 5: Apply conservation of momentum
According to the conservation of momentum:
Initial momentum=Final momentum
Thus, we have:
mv=2mu
Step 6: Solve for u
From the equation mv=2mu, we can simplify:
v=2u
Now, solving for u:
u=v2
Step 7: Conclusion
The speed with which the system moves just after the collision is:
u=v2
We have:
- A block of mass m hanging on one side of a pulley.
- A pan of mass m on the other side.
- A particle of mass m falling onto the pan with an initial speed v.
We will take the downward direction as positive. Therefore:
- The velocity of the falling particle just before impact is +v.
- The initial velocity of the pan and block is 0.
When the particle strikes the pan and sticks to it, we need to consider the change in momentum due to the collision.
Before the collision, the momentum of the system is only due to the falling particle:
Initial momentum=mv
After the collision, the combined mass (particle + pan) moves together with some velocity u:
Final momentum=(m+m)u=2mu
According to the conservation of momentum:
Initial momentum=Final momentum
Thus, we have:
mv=2mu
From the equation mv=2mu, we can simplify:
v=2u
Now, solving for u:
u=v2
The speed with which the system moves just after the collision is:
u=v2
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -1
18 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Exercises
64 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- CALORIMETRYBOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer
9 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
Similar Questions
Two masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)

View SolutionTwo masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration

View SolutionTwo unequal masses of 1kg and 2kg are connected by a string going over a clamed light smooth pulley as shown in figure . The system is released from rest .The larger mass is stopped for a moment 1.0s after the system is set in motion.Find the time elapsed before the string is tight again.

View SolutionTwo blocks each of mass 4 kg connected by a light string which is passing over an ideal pulley is as shown in figure. If the system is released from rest then the acceleration (in m/s2) of centre of mass is (g = 10 m/s2)
View SolutionA pan of mass m=1.5kg and a block of mass M=3kg are connected to each other by a light inextensible string, passing over a light pulley as shown in Fig. Initially, the block is resting on a horizontal floor. A ball of mass m0=0.5kg collides with the pan at a speed v0=20m/s. Consider this instant of collision as t=0. Assume collision to be perfectly inelastic. Now, Fig. answer the following questions based on the above information.

Find the velocity of pan + ball system at t=2.6s. Assume that the block comes to rest instantaneously after striking the floor.
View SolutionA pan of mass m=1.5kg and a block of mass M=3kg are connected to each other by a light inextensible string, passing over a light pulley as shown in Fig. Initially, the block is resting on a horizontal floor. A ball of mass m0=0.5kg collides with the pan at a speed v0=20m/s. Consider this instant of collision as t=0. Assume collision to be perfectly inelastic. Now, Fig. answer the following questions based on the above information.

Find the time t at which the block strikes the floor for the first time
View SolutionA pan of mass m=1.5kg and a block of mass M=3kg are connected to each other by a light inextensible string, passing over a light pulley as shown in Fig. Initially, the block is resting on a horizontal floor. A ball of mass m0=0.5kg collides with the pan at a speed v0=20m/s. Consider this instant of collision as t=0. Assume collision to be perfectly inelastic. Now, Fig. answer the following questions based on the above information.

Mark the correct statement(s) for this situation
View SolutionTwo blocks are connected by a long inextensible string passing over an ideal pulley as shown in the figure. If the system is released from rest then the common speed of blocks when block m2 moves a distance I will be
View SolutionTwo bodies of masses m1andm2 are connected by a light string going over a smooth lilght pulley at the end of an incline. The mass1 lies on the incline m2 hangs vertically. The system is t rest. Find the angle of the incline and the fore exerted by the incline on the body of mass m_1.
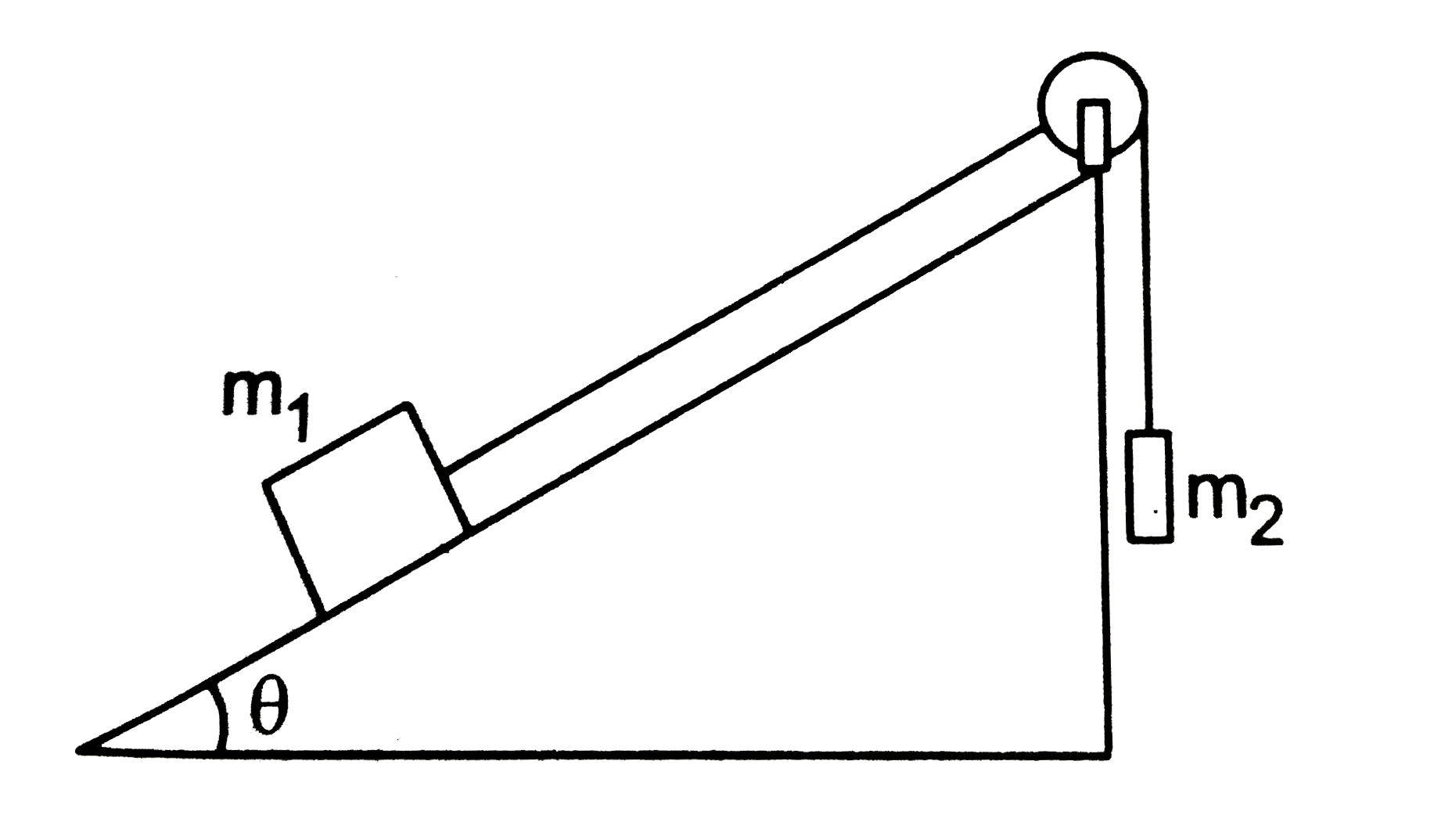
View SolutionTwo blocks A and B of equal masses are attached to a string passing over a smooth pulley fixed to a wedge as shown in figure. Find the magnitude of acceleration of centre of mass of the two blocks when they are released from rest. Neglect friction.

View Solution
