Two block of equal mass m are connected by an unstretched spring and the sytem is kept at rest on a frictionless horizontal surface. A constant force F is applied on one of the blocks puling it away from the other as shown in figure. a.Find the positon of the centre of mass at time t. b.If the extansion of the spring is x0 at time t find the displacement of the two blocks at this instant.
To solve the problem step by step, we will break it down into two parts as requested:
Part (a): Finding the Position of the Center of Mass at Time t
1. Identify the Forces and Masses:
- We have two blocks of equal mass m.
- A constant force F is applied to one of the blocks.
2. Calculate the Acceleration of the Center of Mass:
- The total force acting on the system is F.
- The total mass of the system is 2m.
- The acceleration acm of the center of mass can be calculated using Newton's second law:
acm=Total ForceTotal Mass=F2m
3. Use the Kinematic Equation to Find the Displacement of the Center of Mass:
- The initial velocity u=0 (the system is at rest).
- Using the equation of motion S=ut+12at2:
Scm=0+12(F2m)t2=Ft24m
- Therefore, the position of the center of mass at time t is:
Scm=Ft24m
Part (b): Finding the Displacement of the Two Blocks at Time t
1. Define the Displacements of the Two Blocks:
- Let x1 be the displacement of the first block and x2 be the displacement of the second block.
2. Relate the Displacements to the Center of Mass:
- The position of the center of mass can also be expressed as:
Scm=mx1+mx22m=x1+x22
- Setting this equal to the previously found position of the center of mass:
x1+x22=Ft24m
- Therefore, we have:
x1+x2=Ft22m
3. Express the Extension of the Spring:
- The extension of the spring x0 is given by:
x0=x2−x1
4. Set Up the System of Equations:
- We now have two equations:
1. x1+x2=Ft22m
2. x2−x1=x0
5. Solve the System of Equations:
- Adding the two equations:
(x1+x2)+(x2−x1)=Ft22m+x0
2x2=Ft22m+x0⟹x2=Ft24m+x02
- Subtracting the second equation from the first:
(x1+x2)−(x2−x1)=Ft22m−x0
2x1=Ft22m−x0⟹x1=Ft24m−x02
Final Results:
- The position of the center of mass at time t is:
Scm=Ft24m
- The displacements of the two blocks are:
x1=Ft24m−x02
x2=Ft24m+x02
- We have two blocks of equal mass m.
- A constant force F is applied to one of the blocks.
- The total force acting on the system is F.
- The total mass of the system is 2m.
- The acceleration acm of the center of mass can be calculated using Newton's second law:
acm=Total ForceTotal Mass=F2m
- The initial velocity u=0 (the system is at rest).
- Using the equation of motion S=ut+12at2:
Scm=0+12(F2m)t2=Ft24m
- Therefore, the position of the center of mass at time t is:
Scm=Ft24m
- Let x1 be the displacement of the first block and x2 be the displacement of the second block.
- The position of the center of mass can also be expressed as:
Scm=mx1+mx22m=x1+x22
- Setting this equal to the previously found position of the center of mass:
x1+x22=Ft24m
- Therefore, we have:
x1+x2=Ft22m
- The extension of the spring x0 is given by:
x0=x2−x1
- We now have two equations:
1. x1+x2=Ft22m
2. x2−x1=x0
- Adding the two equations:
(x1+x2)+(x2−x1)=Ft22m+x0
2x2=Ft22m+x0⟹x2=Ft24m+x02
- Subtracting the second equation from the first:
(x1+x2)−(x2−x1)=Ft22m−x0
2x1=Ft22m−x0⟹x1=Ft24m−x02
- The position of the center of mass at time t is:
Scm=Ft24m
- The displacements of the two blocks are:
x1=Ft24m−x02
x2=Ft24m+x02
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -1
18 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Exercises
64 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- CALORIMETRYBOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer
9 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
Similar Questions
Two blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on one of the blocks pulling it away from the other as shown in figure. (a) Find the displacement of the centre of mass at time t. (b) If the extension of the spring is x0 at time t, find the displacement of the two blocks at this instant.

View SolutionTwo blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

Then the displacement of the centre of mass in at time t is
View SolutionTwo blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

If the extension of the spring is x0 at time t, then the displacement of the first block at this instant is
View SolutionTwo blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

If the extension of the spring is x0 at time t, then the displacement of the first block at this instant is
View SolutionTwo blocks each of mass m, connected by an un-stretched spring are kept at rest on a frictionless horizontal surface. A constant force F is applied on one of the blocks pulling it away from the other as shown in figure.
(a)Find accelaration of the mass center.
(b) Find the displacement of the centre of mass as function of time t.
(c) If the extension of the spring is X0 at an instant t, find the displacements of the two blocks relative to the ground at this instant.
View SolutionTwo blocks of masses M1andM2 are placed in contact with each other on a frictionless horizontal surface. If a force F is applied on the block of mass M1, what is the contact force between the two blocks?
View SolutionTwo identical blocks A and B each of mass M are connected to each other through a light string. The system is placed on a smooth horizontal floor. When a constant force F is applied horizontally on the block A, find the tension in the string.
View SolutionAssertion: A constant force F is applied on two blocks and one spring system as shown in figure. Velocity of centre of mass increases linearly with time.

Reason: Acceleration of centre of mass is constant.
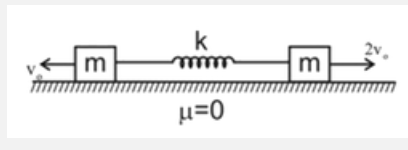
View SolutionThe figure shows two blocks of mass m each, connected by an ideal unstretched spring and then placed on a frictionless floor. If the blocks are given velocities v0and2v0 as shown, then the maximum extension in the spring is
View SolutionA block of mass'm' it kept over the smooth surface of the plank of mass M. the plank of length l is kept over the smooth horizontal surface. A constant horizontal force F is applied onto the plank as shown in figure. Calculate the time after which the block falls off the plank?

View Solution
