A cubical block of ice of mass m and edge L is placed in a large tray of mass M. If the ice melts, how far does the centre of mass of the system ''ice plus tray'' come down?
To solve the problem, we need to find out how far the center of mass of the system (ice plus tray) comes down when the ice melts. Let's break this down step by step.
Step 1: Define the System
We have a cubical block of ice with mass m and edge length L placed in a large tray with mass M.
Step 2: Initial Position of the Center of Mass
Let’s denote the position of the center of mass of the tray as x1 and that of the ice as x2. The center of mass x of the system (ice plus tray) can be calculated using the formula:
x=Mx1+mx2M+m
Step 3: Determine the Initial Positions
Assuming the bottom of the tray is at the reference point (0), the center of mass of the tray is at:
x1=L2
(since the tray's center of mass is at its midpoint).
The center of mass of the ice block (which is also at height L/2 initially) is also at:
x2=L2
Step 4: Calculate Initial Center of Mass
Substituting these values into the center of mass formula, we get:
x=M(L2)+m(L2)M+m=(M+m)(L2)M+m=L2
Step 5: Melting of Ice
When the ice melts, it turns into water. The center of mass of the water will be at the same horizontal position as the ice, but its vertical position will change. The center of mass of the melted water will now be:
x′=x2−L2=L2−L2=0
Step 6: Calculate New Center of Mass
Now, we need to find the new center of mass of the system (water plus tray):
x′=Mx1+mx′M+m=M(L2)+m(0)M+m=M(L2)M+m
Step 7: Find the Change in Center of Mass
To find how far the center of mass has come down, we need to calculate the difference between the initial center of mass and the new center of mass:
Δx=x−x′=L2−M(L2)M+m
Simplifying this gives:
Δx=L2(1−MM+m)=L2(mM+m)=mL2(M+m)
Final Answer
Thus, the center of mass of the system comes down by:
Δx=mL2(M+m)
We have a cubical block of ice with mass m and edge length L placed in a large tray with mass M.
Let’s denote the position of the center of mass of the tray as x1 and that of the ice as x2. The center of mass x of the system (ice plus tray) can be calculated using the formula:
x=Mx1+mx2M+m
Assuming the bottom of the tray is at the reference point (0), the center of mass of the tray is at:
x1=L2
(since the tray's center of mass is at its midpoint).
x2=L2
Substituting these values into the center of mass formula, we get:
x=M(L2)+m(L2)M+m=(M+m)(L2)M+m=L2
When the ice melts, it turns into water. The center of mass of the water will be at the same horizontal position as the ice, but its vertical position will change. The center of mass of the melted water will now be:
x′=x2−L2=L2−L2=0
Now, we need to find the new center of mass of the system (water plus tray):
x′=Mx1+mx′M+m=M(L2)+m(0)M+m=M(L2)M+m
To find how far the center of mass has come down, we need to calculate the difference between the initial center of mass and the new center of mass:
Δx=x−x′=L2−M(L2)M+m
Simplifying this gives:
Δx=L2(1−MM+m)=L2(mM+m)=mL2(M+m)
Thus, the center of mass of the system comes down by:
Δx=mL2(M+m)
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -1
18 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Exercises
64 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- CALORIMETRYBOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer
9 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
Similar Questions
Consider a gravity free hall in which a tray of mas M, carrying a cubical block of ice of mass m and edge L, is at rest in the middle.. If the ice melts, by what distance does the centre of mass of the tray plus the ice system descend?
View SolutionA bullet of mass m and velocity v is fired into a large block of mass M. The final velocity of the system is
View SolutionA block of mass m slides over a smooth wedge of mass M which is placed over a rough horizontal surface . The centre of mass of the system will move towards left

Here μ = coefficient of friction between the wedge and the ground .
View SolutionFour point masses are placed at the corners of a square of side 2 m as shown in the figure. Find the centre of mass of the system w.r.t. the centre of square.

View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

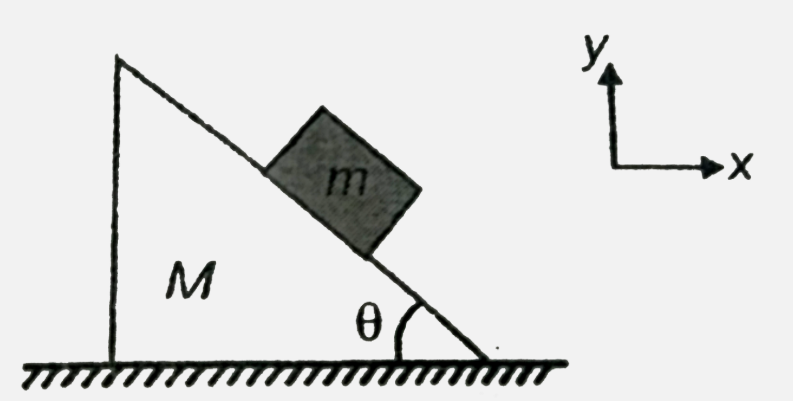
View SolutionA block of mass m is placed on a smooth wedge of mass M, as shown in the figure . Just after placiing block m over wedge M.
View SolutionA cubical block of mass M and edge a slides down a rougg inclined plane of inclination θ with a uniform velocity. The torque of the normal force on the block about its centre has magnitude.
View SolutionA cubical block of mass M and edge a slides down a rougg inclined plane of inclination θ with a uniform velocity. The torque of the normal force on the block about its centre has magnitude.
View SolutionIn a free space a rifle on mass M shoots a bullet of mass m at a stationary block of mass M distance D away from it . When the bullet has moved through a distance d towards the block the centre of mass of the bullet − block system is at a distance of :
View SolutionA block of mass 3M connected to a massless rod of length L lies at rest on a fixed frictionless table. A second block of mass M moving with speed v0 strikes the opposite end of the rod at right angle and sticks. The velocity of centre of mass of the system after collision is
_PHY_E05_239_Q01.png)
View Solution
