The heavier block in an atwood machine has a mass twice that of the lighter one. The tension in the string is 16.0 N when the system is set into motion. Find the decrease in the gravitational potential energy during the first second after the system is released from rest.
The correct Answer is:A
To solve the problem of finding the decrease in gravitational potential energy during the first second after the Atwood machine system is released from rest, we can follow these steps:
1. Identify the Masses:
Let the mass of the lighter block be m. Therefore, the mass of the heavier block will be 2m.
2. Write the Forces Acting on Each Block:
- For the heavier block (mass 2m):
Fnet, heavy=2mg−T=2ma
- For the lighter block (mass m):
Fnet, light=T−mg=ma
3. Combine the Equations:
Adding the two equations:
(2mg−T)+(T−mg)=2ma+ma
This simplifies to:
mg=3ma
Therefore, we can express the acceleration a as:
a=g3
4. Use the Given Tension:
The tension T in the string is given as 16.0N. We can use this to find mg:
From the equation for the lighter block:
T−mg=ma
Substituting a from above:
16−mg=m(g3)
Rearranging gives:
mg+mg3=16
This simplifies to:
4mg3=16
Therefore:
mg=12N
5. Calculate the Displacement:
The displacement S of the heavier block during the first second can be calculated using the second equation of motion:
S=ut+12at2
Since the initial velocity u=0 and t=1s:
S=0+12(g3)(12)=g6
6. Calculate the Decrease in Potential Energy:
The decrease in gravitational potential energy ΔPE for the heavier block (which moves downward) is given by:
ΔPE=Weight×Displacement=(2m⋅g)⋅S
Substituting mg=12N gives:
ΔPE=2⋅12⋅g6
Since g≈10m/s2:
ΔPE=2⋅12⋅106=20J
Final Answer:
The decrease in gravitational potential energy during the first second after the system is released from rest is 20 Joules.
Let the mass of the lighter block be m. Therefore, the mass of the heavier block will be 2m.
- For the heavier block (mass 2m):
Fnet, heavy=2mg−T=2ma
- For the lighter block (mass m):
Fnet, light=T−mg=ma
Adding the two equations:
(2mg−T)+(T−mg)=2ma+ma
This simplifies to:
mg=3ma
Therefore, we can express the acceleration a as:
a=g3
The tension T in the string is given as 16.0N. We can use this to find mg:
From the equation for the lighter block:
T−mg=ma
Substituting a from above:
16−mg=m(g3)
Rearranging gives:
mg+mg3=16
This simplifies to:
4mg3=16
Therefore:
mg=12N
The displacement S of the heavier block during the first second can be calculated using the second equation of motion:
S=ut+12at2
Since the initial velocity u=0 and t=1s:
S=0+12(g3)(12)=g6
The decrease in gravitational potential energy ΔPE for the heavier block (which moves downward) is given by:
ΔPE=Weight×Displacement=(2m⋅g)⋅S
Substituting mg=12N gives:
ΔPE=2⋅12⋅g6
Since g≈10m/s2:
ΔPE=2⋅12⋅106=20J
The decrease in gravitational potential energy during the first second after the system is released from rest is 20 Joules.
Topper's Solved these Questions
- WORK AND ENERGYBook:HC VERMA ENGLISHChapter:WORK AND ENERGYExercise:Question for Short Answer
Explore 16 Videos
- WORK AND ENERGYBook:HC VERMA ENGLISHChapter:WORK AND ENERGYExercise:Objective -2
Explore 8 Videos
- WAVE MOTION AND WAVES ON A STRINGBook:HC VERMA ENGLISHChapter:WAVE MOTION AND WAVES ON A STRINGExercise:Question for short Answer
Explore 7 Videos
Similar Questions
The two blocks in an Atwood machine have masses 2.0 kg and 3.0 kg. Find the work done by gravity during the fourth second after the system is released from rest.
View SolutionIn the ideal atwood machine arrangement shown, what is the change in kinetic energy of the system in 1√2second of their motion starting from rest ?
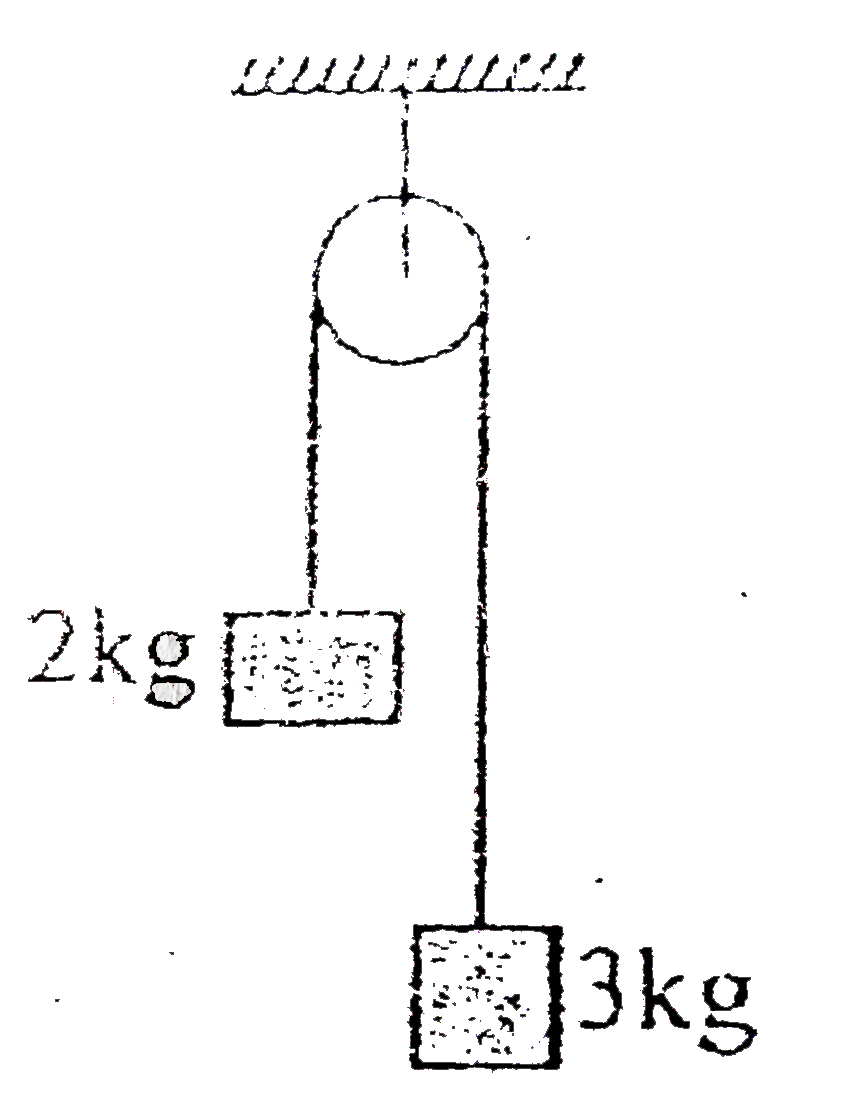
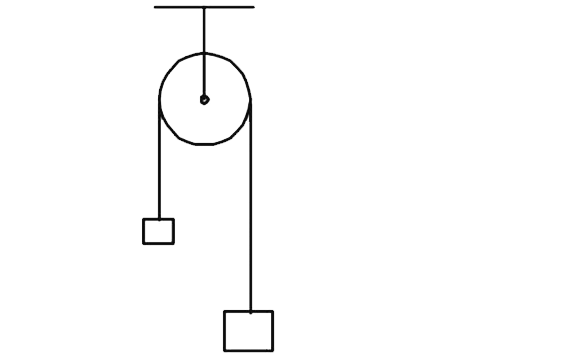
View SolutionA light inextensible string that gas over a smoth fixed polley as shown in the figure connect two blocks of mases it 0.36 kg and 0.72 kg Taking g=10ms−2 , find the work done by the string on the block of mass 0.36 kg doring the first second after the system is released from rest ,
View SolutionA block of mass m can slide freely along the verticle surface of a bigger block of mass M as shown in fig. There is no friction anywhere in the system. The block m is connected to one end is fixed at point P.
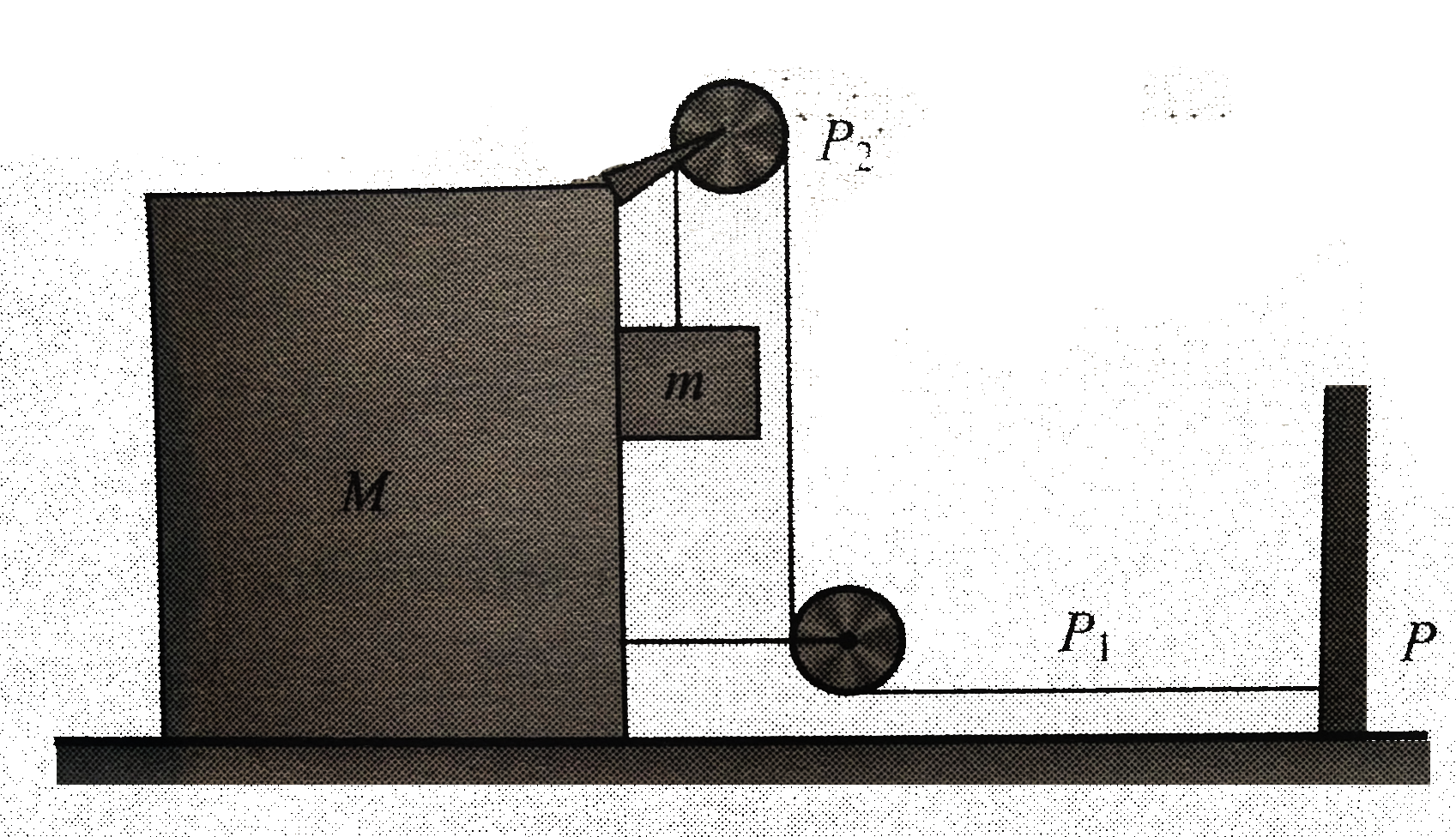
The string between P1 and P is horizontal and other parts of the string are vertical. system is released from rest. Find the acceleration of m and M during their subsequent motion.
View SolutionA big block of mass M is placed on a horizontal surface. Two cubes each of mass m are attached with ideal string-pulley system as shown in figure. On ecube falls in the groove drilled into the block as shown. Assuming all the surfaces are smooth and system is released from rest, find instantaneous power developed by gravity. (consider M=2m). Assume that the system starts moving from rest at time t = 0 .

View SolutionA string 25cm long and having a mass of 2.5gm is under tension. A pipe closed at one end is 40cm long. When the string is set vibrating in its first overtone and the air in the pipe in its fundamental frequency, 8 beats per second are heard. It is observed that decreasing the tension in the string decreases beat frequency. If the speed of sound in air is 320m/s, find the tension in the string.
View SolutionA string 25cm long and having a mass of 2.5gm is under tension. A pipe closed at one end is 40cm long. When the string is set vibrating in its first overtone and the air in the pipe in its fundamental frequency, 8 beats per second are heard. It is observed that decreasing the tension in the string decreases beat frequency. If the speed of sound in air is 320m/s, find the tension in the string.
View SolutionTwo blocks of masses m1=2kg and m2=4kg are attached to two ends of a light ideal spring of force constant k = 1000 N/m. The system is kept on a smooth inclined plane inclined at 30∘ with horizontal. The block m2 is attached to a light string whose other end is connected to a mass m3=1kg. A force F = 15N is applied on m1 and the system is released from rest. Assume initially the spring is at relaxed position and the system is released from rest. Find the
(a) maximum extension of the spring.
(

View SolutionIn Fig. a pulley is shown which is frictionless and a ring of mass m can slide on the string without any friction. One end of the string is attached to point B and to the other end, a block 'P' of mass m is attached. The whole system lies in vertical plane.
 If the system is released from rest, it is found that the system remains at rest. What is the value of θ
If the system is released from rest, it is found that the system remains at rest. What is the value of θ
View SolutionA block B of mass M is suspended from a cord of length l attached to a cart A of mass M as shown in the figure. The horizontal surface on which the cart moves is smooth. Initially both the cart and the block are at rest in the position shown. Now B is released. Take M=m=2kg,θ=45∘andg=10m/s2.
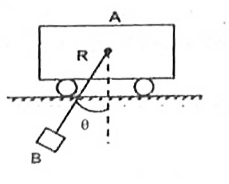
The tension in the cord immediately after the system is released from rest is
View Solution

