A particle moves rom a point →r1=(2m)→i+(3m)→j to another point →r2=(3m)→i+(2m)→j during which a certain force →F=(5N)→i+(5N)→j acts on it. Find the work done by the force on the particle during the displacement.
To find the work done by the force on the particle during its displacement, we can follow these steps:
Step 1: Identify the initial and final position vectors.
The initial position vector is given as:
→r1=(2m)^i+(3m)^j
The final position vector is given as:
→r2=(3m)^i+(2m)^j
Step 2: Calculate the displacement vector.
The displacement vector Δ→r can be calculated as:
Δ→r=→r2−→r1
Substituting the values:
Δ→r=((3m)^i+(2m)^j)−((2m)^i+(3m)^j)
Calculating the components:
Δ→r=(3−2)^i+(2−3)^j=(1m)^i−(1m)^j
Step 3: Identify the force vector.
The force vector is given as:
→F=(5N)^i+(5N)^j
Step 4: Calculate the work done by the force.
The work done W by the force during the displacement is given by the dot product of the force vector and the displacement vector:
W=→F⋅Δ→r
Substituting the vectors:
W=((5N)^i+(5N)^j)⋅((1m)^i−(1m)^j)
Calculating the dot product:
W=(5N⋅1m)+(5N⋅−1m)=5−5=0J
Final Answer:
The work done by the force on the particle during the displacement is:
0J
The initial position vector is given as:
→r1=(2m)^i+(3m)^j
The final position vector is given as:
→r2=(3m)^i+(2m)^j
The displacement vector Δ→r can be calculated as:
Δ→r=→r2−→r1
Substituting the values:
Δ→r=((3m)^i+(2m)^j)−((2m)^i+(3m)^j)
Calculating the components:
Δ→r=(3−2)^i+(2−3)^j=(1m)^i−(1m)^j
The force vector is given as:
→F=(5N)^i+(5N)^j
The work done W by the force during the displacement is given by the dot product of the force vector and the displacement vector:
W=→F⋅Δ→r
Substituting the vectors:
W=((5N)^i+(5N)^j)⋅((1m)^i−(1m)^j)
Calculating the dot product:
W=(5N⋅1m)+(5N⋅−1m)=5−5=0J
The work done by the force on the particle during the displacement is:
0J
Topper's Solved these Questions
- WORK AND ENERGYBook:HC VERMA ENGLISHChapter:WORK AND ENERGYExercise:Question for Short Answer
Explore 16 Videos
- WORK AND ENERGYBook:HC VERMA ENGLISHChapter:WORK AND ENERGYExercise:Objective -2
Explore 8 Videos
- WAVE MOTION AND WAVES ON A STRINGBook:HC VERMA ENGLISHChapter:WAVE MOTION AND WAVES ON A STRINGExercise:Question for short Answer
Explore 7 Videos
Similar Questions
A particle moves from a point (2m,3m,0) to (3m,2m,0) under the action of force of magnitude 5N acting along the line y=x. The work done by the force on the particle during the displacement is
View SolutionForce acting on a particle varies with displacement as shown is Fig. Find the work done by this force on the particle from x=−4m to x = + 4m.
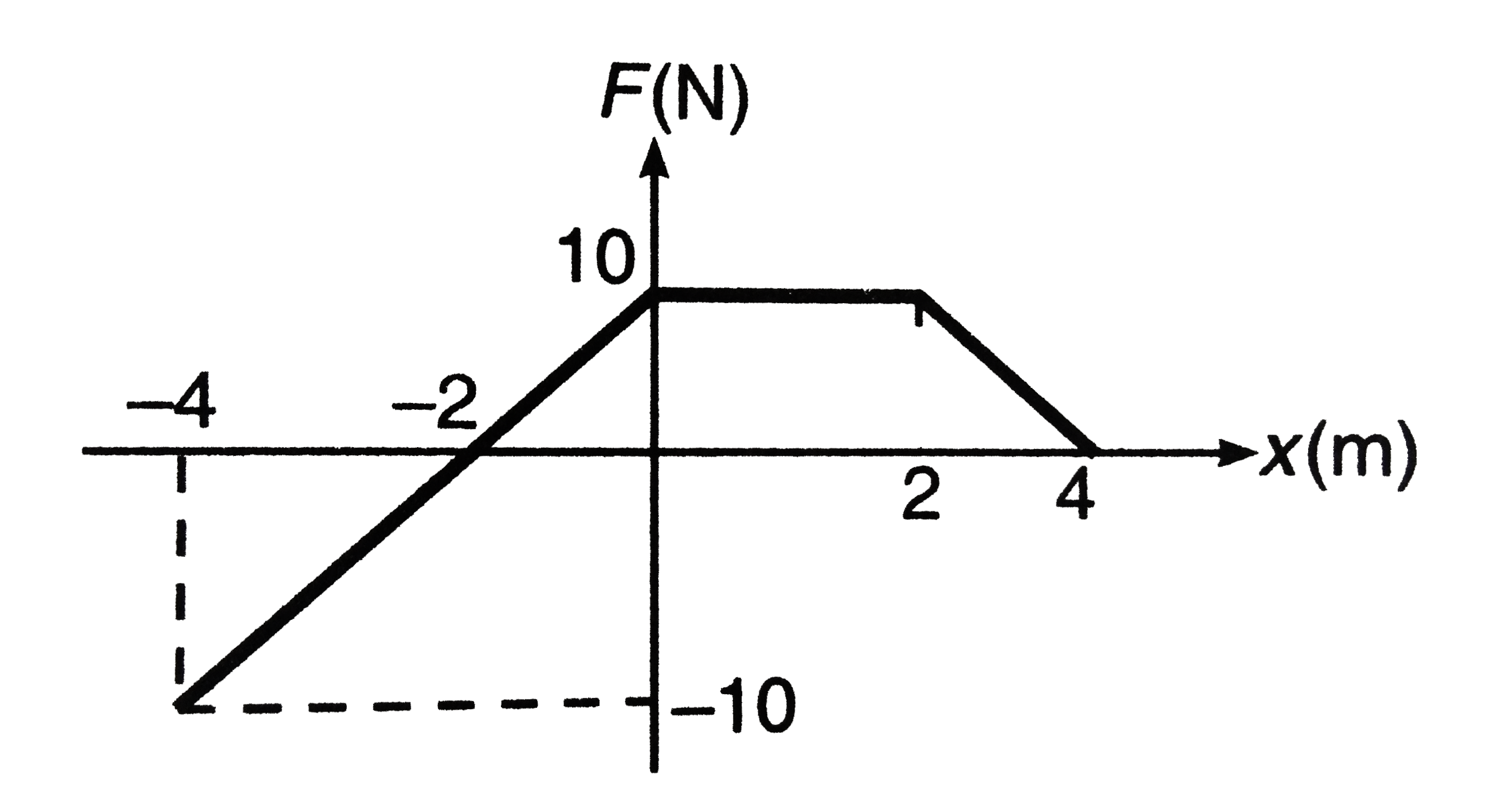 .
.
View SolutionAn object is displaced from point A(2m,3m,4m) to a point B(1m,2m,3m) under a constant force F=(2ˆi+3ˆj+4ˆk)N. Find the work done by this force in this process.
View SolutionForce F on a particle moving in a straight line varies with distance d as shown in the figure. The work done on the particle during its displacement of 12m is
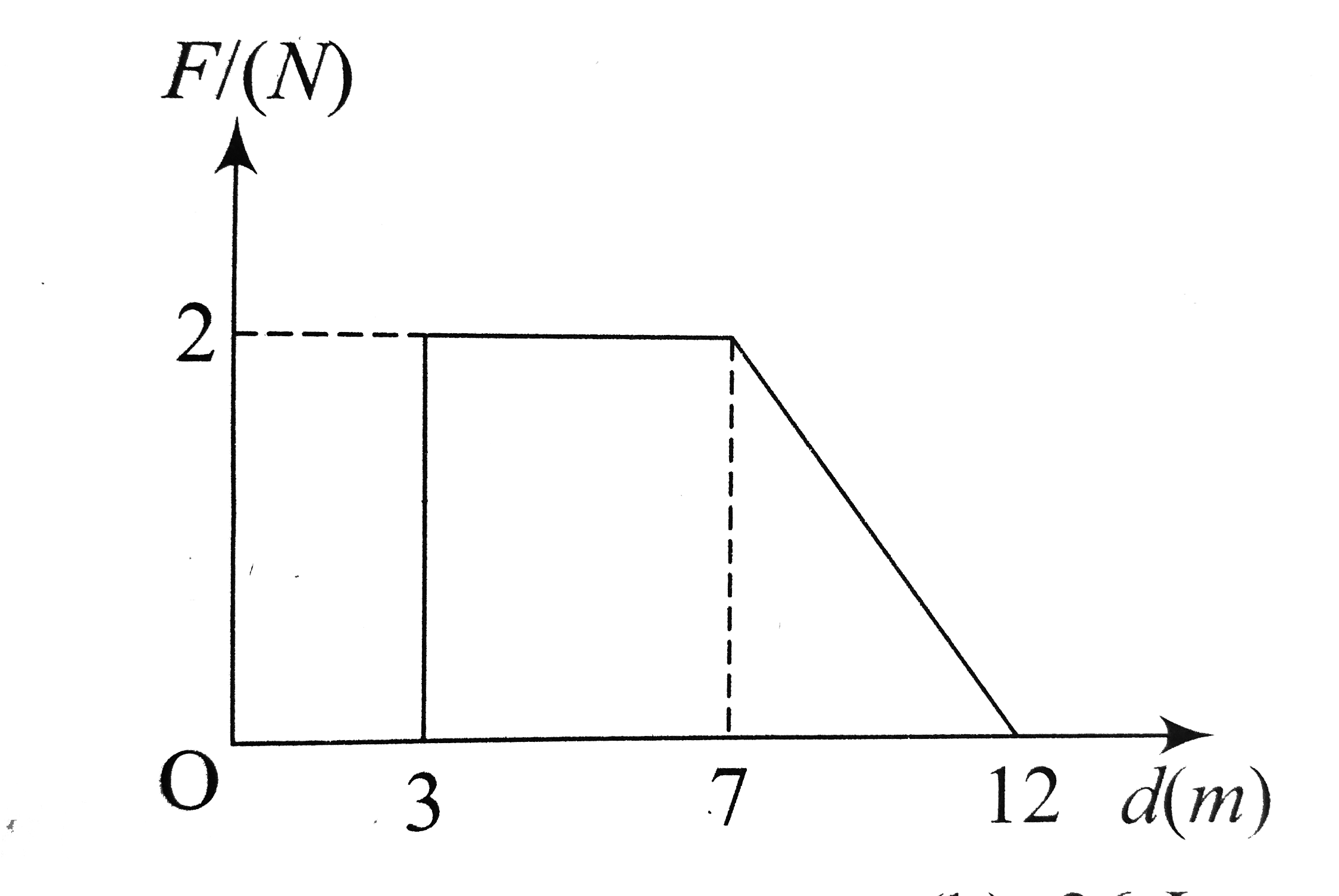
View SolutionAn object is displaced from point A(2m,3m,4m,) to a point B (1m,2m,3m) under a constant force (2ˆi+3ˆj+4ˆk) N. Find the work done by this force in this process.
View SolutionA particle experience a force of 10 N which is constant in magnitude and is always acting towards origin. Calculate the work done by the force on the particle during its displacement from (1,2,3) to (−1,−2,3):
View SolutionA force F=(5+2x) acts on a particle in x direction where F is in Newtown and x is in meter. Find the work done by this force during displacement from x=0 to x=1m.
View SolutionAn object is displaced from a point A(0, 0, 0) to B(1m, 1m , 1m) under a force →F=(yˆi+xˆj)N. Find the work done by this force in this process.
View SolutionA particle moves 5m in the +x direction while being acted upon by a constant force→F=(4N)ˆi+(2N)ˆj−(4N)ˆk . The work done on the particle by this force is
View SolutionA force F=(5+2x) acts on a particle in x direction where F is in newtown and x is meter. Find the work done by this force during displacement from x=0 to x=1m.
View Solution

