A small block of mass 100 g moves wth uniform speed n a horizontal circular groove, with vertical side walls, of radisu 25 cm.If the block takes 2.0 s to complete ne round, find the normal contact force by tehside wall of the groove.
To solve the problem, we need to find the normal contact force exerted by the side wall of the groove on the block. This normal force acts as the centripetal force that keeps the block moving in a circular path.
1. Convert Mass to Kilograms:
The mass of the block is given as 100 g. We need to convert this to kilograms for standard SI units.
m=100g=0.1kg
2. Determine the Radius in Meters:
The radius of the circular groove is given as 25 cm. We convert this to meters.
r=25cm=0.25m
3. Calculate the Angular Velocity:
The block takes 2 seconds to complete one round. The angular velocity (ω) can be calculated using the formula:
ω=2πT
where T is the time period (2 seconds).
ω=2π2=πrad/s
4. Calculate the Centripetal Acceleration:
The centripetal acceleration (ac) can be calculated using the formula:
ac=ω2r
Substituting the values:
ac=(π)2×0.25
ac≈9.87×0.25≈2.4675m/s2
5. Calculate the Centripetal Force:
The centripetal force (Fc) required to keep the block moving in a circle is given by:
Fc=m⋅ac
Substituting the values:
Fc=0.1kg×2.4675m/s2≈0.24675N
6. Normal Contact Force:
The normal contact force exerted by the side wall of the groove is equal to the centripetal force required to keep the block in circular motion. Therefore, the normal contact force is:
Fn=Fc≈0.24675N
Final Answer:
The normal contact force by the side wall of the groove is approximately 0.25 N.
The mass of the block is given as 100 g. We need to convert this to kilograms for standard SI units.
m=100g=0.1kg
The radius of the circular groove is given as 25 cm. We convert this to meters.
r=25cm=0.25m
The block takes 2 seconds to complete one round. The angular velocity (ω) can be calculated using the formula:
ω=2πT
where T is the time period (2 seconds).
ω=2π2=πrad/s
The centripetal acceleration (ac) can be calculated using the formula:
ac=ω2r
Substituting the values:
ac=(π)2×0.25
ac≈9.87×0.25≈2.4675m/s2
The centripetal force (Fc) required to keep the block moving in a circle is given by:
Fc=m⋅ac
Substituting the values:
Fc=0.1kg×2.4675m/s2≈0.24675N
The normal contact force exerted by the side wall of the groove is equal to the centripetal force required to keep the block in circular motion. Therefore, the normal contact force is:
Fn=Fc≈0.24675N
The normal contact force by the side wall of the groove is approximately 0.25 N.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - worked out Examples13videos
CIRCULAR MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Objective -116videos
CIRCULAR MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -211videos
CENTRE OF MASS, LINEAR MOMENTUM, COLLISION
- BOOK - HC VERMA ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - All Questions90videos
FLUID MECHANICS
Similar Questions
A small block of mass 100g moves with uniform speed in a horizontal circular groove, with vertical side walls of radius 25cm. If the block takes 2.0s to complete one round, find the constant force by the side wall of the groove.
View SolutionA car moving at a speed of 36 km/hr is taking a turn on a circular road of radius 50 m. A small wooden plate is kept on the seat with its plane perpendicular to the radius of the circular road figure. A small bock of mass 100 g is kept on the seat which rests against the plate. The friction coefficient between the block and the plate is μ=0.58. a. Find the normal contact force exerted by the plate on the block. b. The plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases Find the angle at which the block will just start sliding on the plate.
 View Solution
View SolutionA block of mass 10kg is placed on a horizontal surface as shown in the figure and a force F=100N is applied on the block as shown, in the figure. The block is at rest with respect to ground. If the contact force between block and ground is 25n (in Newton) then value of n is : (Takeg=10m/s2)
 View Solution
View SolutionA block is mass m moves on as horizontal circle against the wall of a cylindrical room of radius R. The floor of the room on which the block moves is smooth but the friction coefficient between the wall and the block is μ. The block is given an initial speed v0. As a function of the speed v write a. the normal force by the wall on the block. b. the frictional force by the wall and c. the tangential acceleration of the block. d. Integrate the tangential acceleration (dvdt=vdvds) to obtain the speed of the block after one revoluton.
View SolutionThe ball of mas m moves with speed v againest a smooth , fixed vertical circular groove of radius R kept on smooth horizontal surface find the
a. normal reaction of the floor or the ball.
b. normal reaction of the vertical wall on the ball.View SolutionA block of mass √3/10kg is placed on a rough horizontal surface as shown in the figure. A force of 1N is applied at one end of the block and the block remains stationary. The normal force exerted by the sruface on the block acts(g=10m/s2)
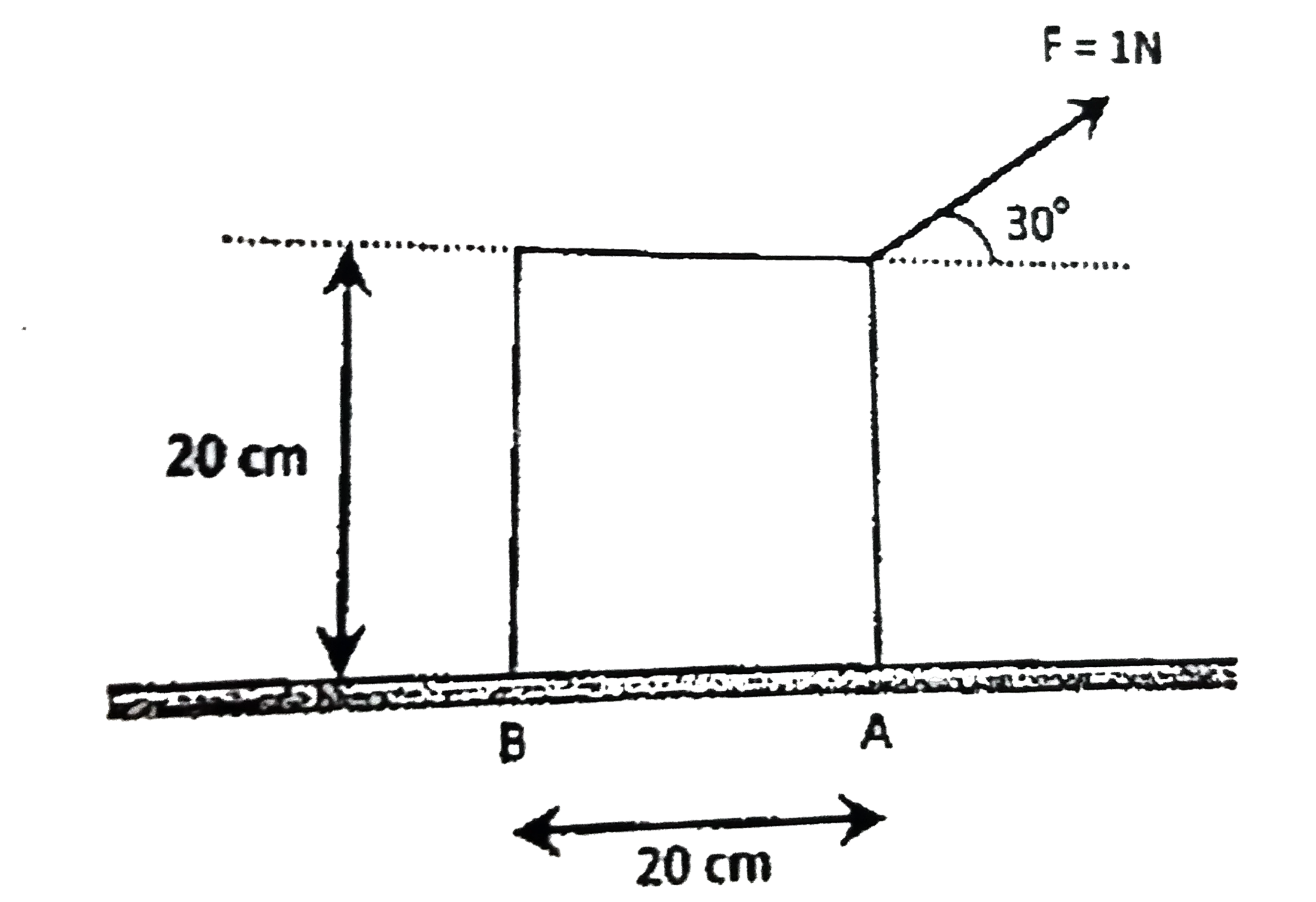 View Solution
View SolutionA small block of mass 1kg is kept on a rough inclined wedge of inclination 45∘ fixed in an elevator. The elevator goes up with a uniform velocity v=2m/s and the block does not slide on the wedge. Find the work done by the force of friction on the block in 1s. (g=10m/s2)
View SolutionA block of mass 1 kg is pushed against a rough vertical wall of μ=0.1
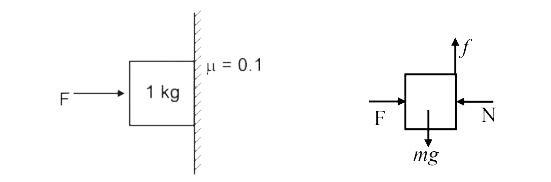
For F = 150, 50 or 100 N the force of friction on the blocks is respectively :View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View Solution
