Raindrops of raidus 1mm and mass 4 mg are falling with a speed of 30 m/s on the head of a bald person. The drops splash on the head and come to rest. Assuming equivaletly that the drops cover a distance equal to their radii on the head, estimate the force exerted by the each drop on the head.
To solve the problem of estimating the force exerted by each raindrop on the head of a bald person, we can follow these steps:
Step 1: Identify the given data
- Radius of the raindrop, r=1mm=1×10−3m
- Mass of the raindrop, m=4mg=4×10−6kg
- Initial speed of the raindrop, u=30m/s
- Final speed of the raindrop when it comes to rest, v=0m/s
Step 2: Calculate the distance traveled by the raindrop before coming to rest
The distance traveled by the raindrop before it comes to rest is equal to its radius:
- Distance, s=r=1×10−3m
Step 3: Use the third equation of motion to find acceleration
We can use the third equation of motion:
v2=u2+2as
Substituting the known values:
0=(30)2+2a(1×10−3)
This simplifies to:
0=900+2a(1×10−3)
Rearranging gives:
2a(1×10−3)=−900
a=−9002×1×10−3=−9002×10−3=−450000m/s2
Step 4: Calculate the force exerted by the raindrop
Using Newton's second law, the force F can be calculated as:
F=m⋅a
Substituting the values:
F=(4×10−6kg)⋅(−450000m/s2)
Calculating this gives:
F=−1.8N
Since force is a vector, we can ignore the negative sign when considering magnitude, so the force exerted by each drop on the head is 1.8N.
Final Answer
The force exerted by each raindrop on the head is 1.8N.
---
- Radius of the raindrop, r=1mm=1×10−3m
- Mass of the raindrop, m=4mg=4×10−6kg
- Initial speed of the raindrop, u=30m/s
- Final speed of the raindrop when it comes to rest, v=0m/s
The distance traveled by the raindrop before it comes to rest is equal to its radius:
- Distance, s=r=1×10−3m
We can use the third equation of motion:
v2=u2+2as
Substituting the known values:
0=(30)2+2a(1×10−3)
This simplifies to:
0=900+2a(1×10−3)
Rearranging gives:
2a(1×10−3)=−900
a=−9002×1×10−3=−9002×10−3=−450000m/s2
Using Newton's second law, the force F can be calculated as:
F=m⋅a
Substituting the values:
F=(4×10−6kg)⋅(−450000m/s2)
Calculating this gives:
F=−1.8N
Since force is a vector, we can ignore the negative sign when considering magnitude, so the force exerted by each drop on the head is 1.8N.
The force exerted by each raindrop on the head is 1.8N.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Questions for short Answer
17 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective -2
9 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMA ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - All Questions
64 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer
14 Videos
Similar Questions
An iron nail of mass m is dropped from a height h from level of a sand bed. If it penetrates through a distance x in the sand before coming to rest. Calculate the average force exerted by the sand on the nail. (Take g=10m/s2)
View Solution(b) Two balls each of mass m moving in opposite direction with equal speed v collide head -on with each other . Predict the outcome of the collision assuming it perfectly elastic.
View Solution
Knowledge Check
A raindrop of mass 1 g falling from a height of 1 km hits the ground with a speed of 50ms−1. If the resistive force is proportional to the speed of the drop, then the work done by the resistive force is (Take g=10ms−2)
A10 JB-10 JC8.75JD−8.75J
Ram and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
The ratio of the energy consumed by the camel during uniform motion for the two cases when it moves with speed 5ms−1 to the case when it moves with 10ms−1
View SolutionRam and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
Sign of work done by the camel on the load during parts of motion, accelerated motion, uniform motion and retarded motion, respectively are
View SolutionA raindrop of radius 0.2 mm falls through air: If the viscosity of air is 18 ×10−6 Pl, find the viscous drag acting on the drop when its speed is 1 m s−1.
View SolutionTwo identical balls each of mass 4 kg are moving towards each other with speeds 2 m/s and 3 m/s respectively. They undergo head on perfectly elastic collision. Then impulse imparted by one ball on other is
View SolutionConsider a drop of rain water having mass 1 g falling from a height of 1km. It hits the ground with a speed of 50m/s Take g constant with a volume 10m/s2. The work done by the
(i) gravitational force and the
(ii) resistive force of air is :
View SolutionConsider a drop of rain water having mass 1 g falling from a height of 1km. It hits the ground with a speed of 50m/s Take g constant with a volume 10m/s2. The work done by the
(i) gravitational force and the
(ii) resistive force of air is :
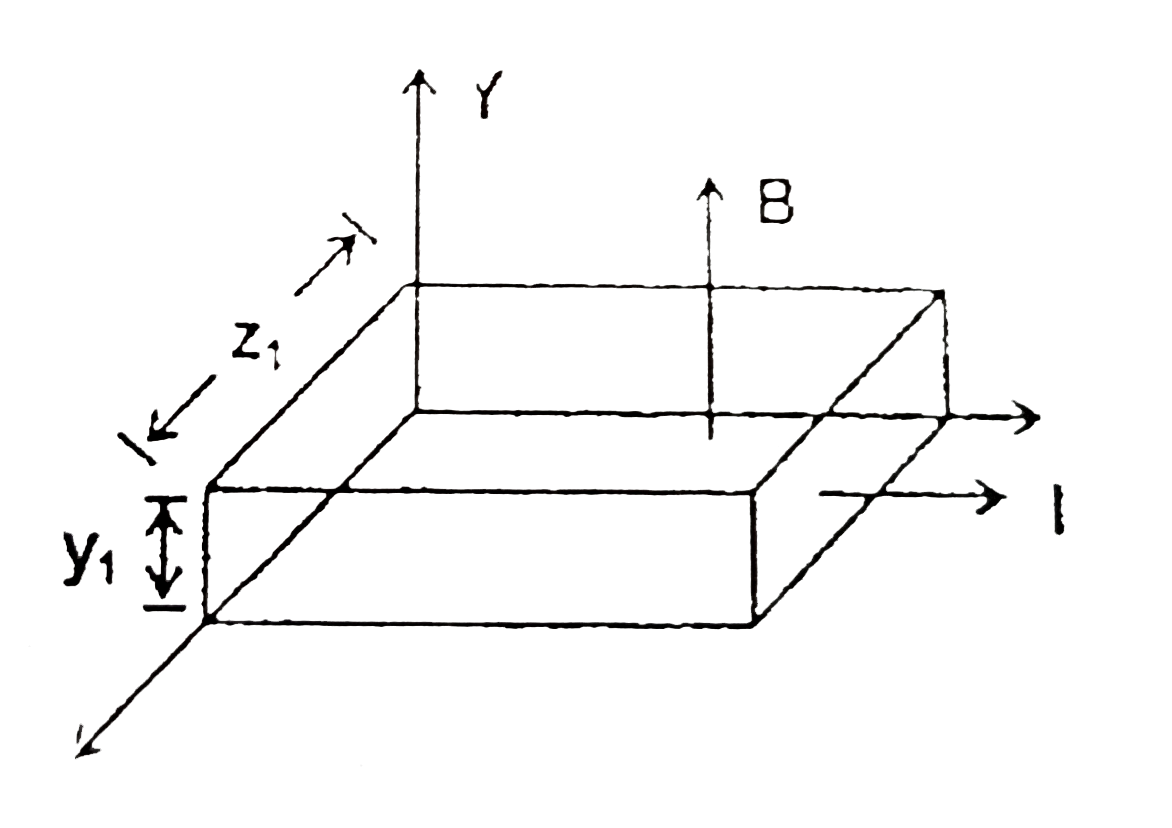
View SolutionThe basic principle underlying the Hall effect is the Lorentz force. When an electron moves along a direction perpendicular to an applied magnetic field, it experiences a force acting normal to both the directions and moves in response to this force and the force exerted by the internal electric field. For an n-type, bar-shaped semiconductor, the carriers are predominantly electrons of bulk density n. We assume that the constant current I flows along the x-axis from left to right in the presence of a magnetic field toward y-axis. Electrons subjected to the lorentz force initially drift away from the current line toward the negative z-axis, resulting in an excess surface electrical charge on the sides of the sample. This charge results in the hall voltage, a potential drop across the two sides of the sample.
The transverse voltage is the hall voltage VH and its magnitude is equal to IB/qnd, where I is the current, B is the magnetic field, d is the sample thickness and q is the elementary charge. A silver ribbon lies as shown in the adjacent figure. (z1=11.8mm and y1=0.23mm) carrying a current of 120A in the x-direction in a uniform magnetic field B=0.95T. If electron density is 5.85×1028/m3, then
Magnitude of the drift velocity of elelctrons is
View Solution

