In a simple Atwood machine, two unequal masses m1andm2 are connected by string going over a clamped light smooth pulley . In a typical arrangement m1=300g and m2=600g. The system is released from rest. (a) Find the distance travelled by the first block in first two seconds. (b) Find the tension in the string. (c) Find the force exerted by clamp on the pulley.
Given that m1=0.3kg<br> m_2 = 0.6 kg<br> T-(m_1g+m_1a)=0…….i.<br> rarr t=m-1g+m_1a<br> Again, T+m_2a-m_2g=0…………<br>rarr T=m_2g-m_2a<br> From equations. i. and ii, we have
m1g+m1a+m2a−m2g=0
→a(m1+m2)=g(m2−m1)

a. t=2 sec, acceleration a=3.266 ms^-2
Initial velocity u=0
So, distance traveled by the body
S=ut+12at2
=0+12(3.266)22=6.5m
From equation i.
T=m1(g+a0
=0.3(3.8+3.26)=3.9N<br>Theforceexertedbytheclaponthep≤––––yisgivenby,<br> F-2T=0<br>rarr F=2T=2xx3.9=7.8N.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Questions for short Answer17videos
NEWTON'S LAWS OF MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective -29videos
NEWTON'S LAWS OF MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - All Questions64videos
LAWS OF THERMODYNAMICS
- BOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer14videos
PHYSICS AND MATHEMATICS
Similar Questions
Two unequal masses are connected by a very light string over a clamped light smooth pulley. Find the acceleration of the system and the tension in the string.
View SolutionTwo unequal masses of 1kg and 2kg are connected by a string going over a clamed light smooth pulley as shown in figure . The system is released from rest .The larger mass is stopped for a moment 1.0s after the system is set in motion.Find the time elapsed before the string is tight again.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two masses m1=1kgandm2=2kg are connected by a light inextensible string and suspended by means of a weightness pulley as shown in the figure. Assuming that both the masses start from rest, the distance travelled by the centre of mass in two seconds is (Takeg=10ms−2.
 .Aa. 20/9 mBb. 40/9 mCc. 2/3 mDd. 1/3 m
.Aa. 20/9 mBb. 40/9 mCc. 2/3 mDd. 1/3 m
In a simple Atwood's machine, two unequal masses m1=5kg , m2=2kg are connected by a string going over a clamped light smooth pulley. Now a constant force F = 1 N is applied on each mass in vertically downward direction. The ratio of acceleration of either block before and after applying the force will be
View SolutionTwo bodies of masses 1 kg and 2 kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string
View SolutionTwo bodies of masses m1andm2 are connected by a light string going over a smooth lilght pulley at the end of an incline. The mass1 lies on the incline m2 hangs vertically. The system is t rest. Find the angle of the incline and the fore exerted by the incline on the body of mass m_1.
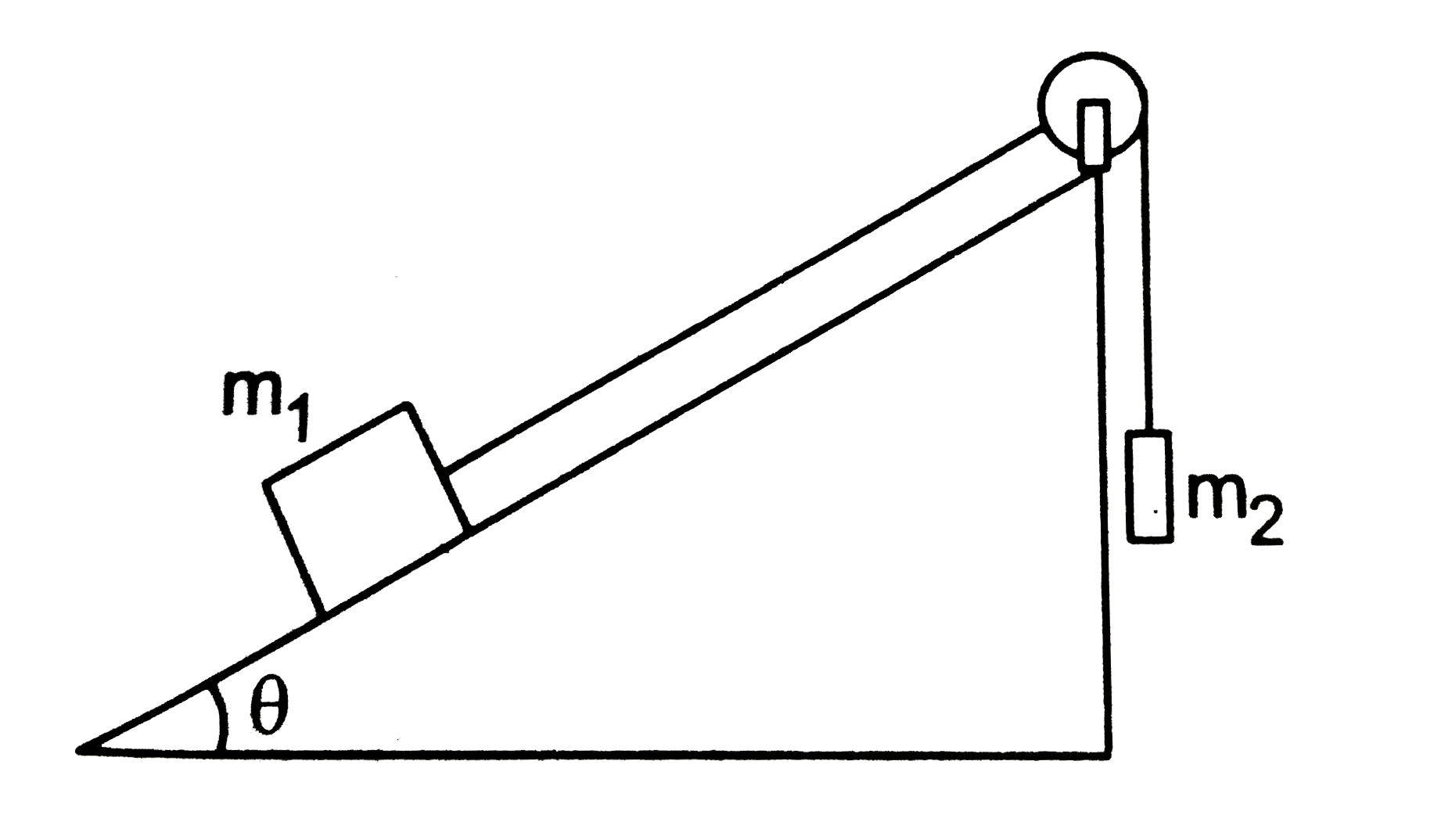 View Solution
View SolutionTwo unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown in figure. If the system is released from rest, find the work done by string on both the blocks in 1 s. (Take g = 10 ms−2)
 View Solution
View SolutionTwo unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown . If the system is released from rest, find the work done by string on both the blocks in 1 s.
(Take g=10m/s2).
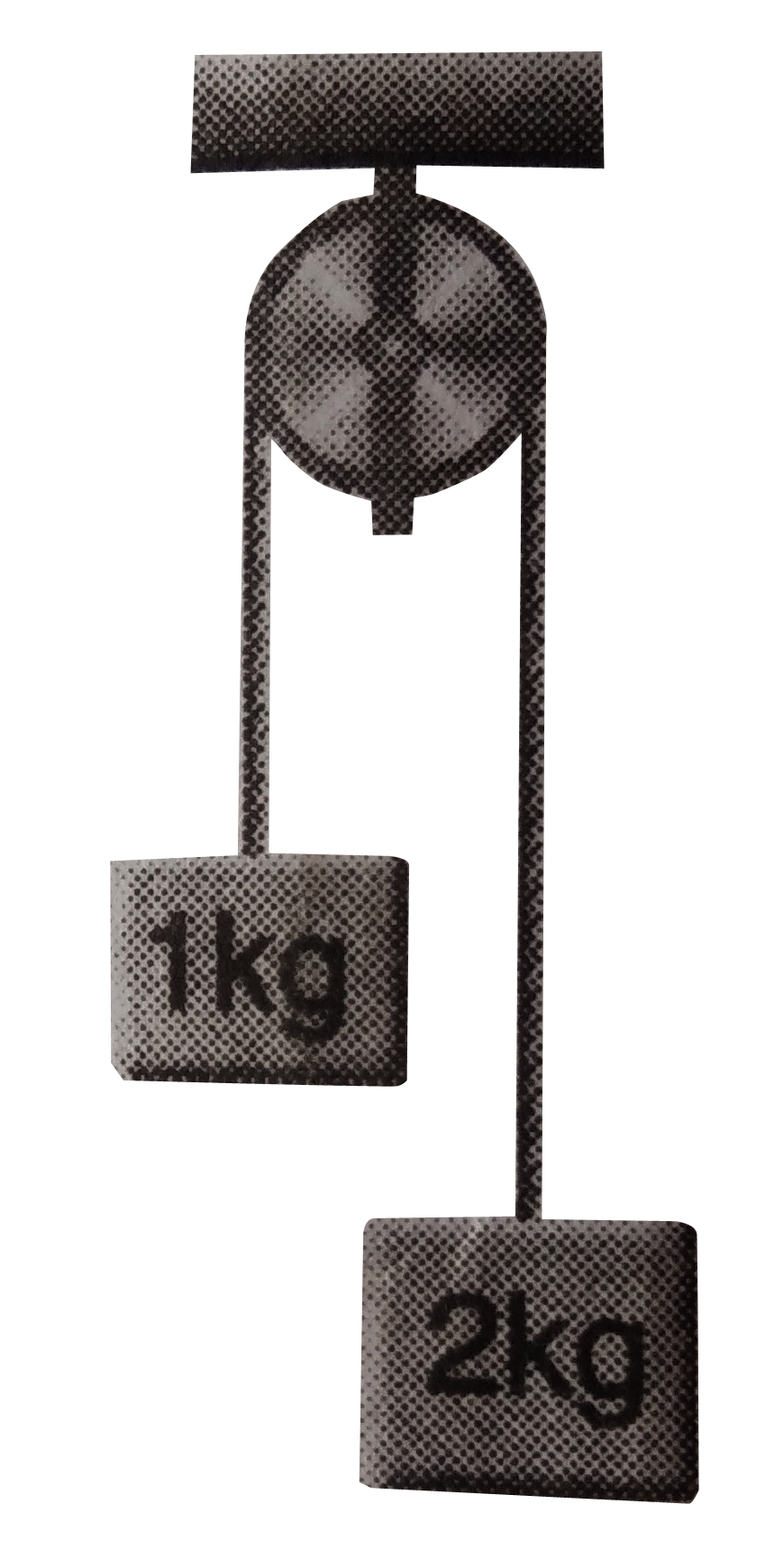 View Solution
View SolutionThe pulley is light and smooth: the strings are inextensible and light. The system is released from rest, find the acceleration of each block, tensions in the strings and reaction in pulley.
 View Solution
View SolutionTwo blocks of masses 2 kg and 4 kg are connected by a light string passing over a light smooth pulley clamped to the edge of a horizontal table. The 2 kg block is on the smooth horizontal table and the other block is hanging vertically, (i) Find the acceleration of the stem if it is released from rest, (ii) Find the tension in the string.
View Solution
