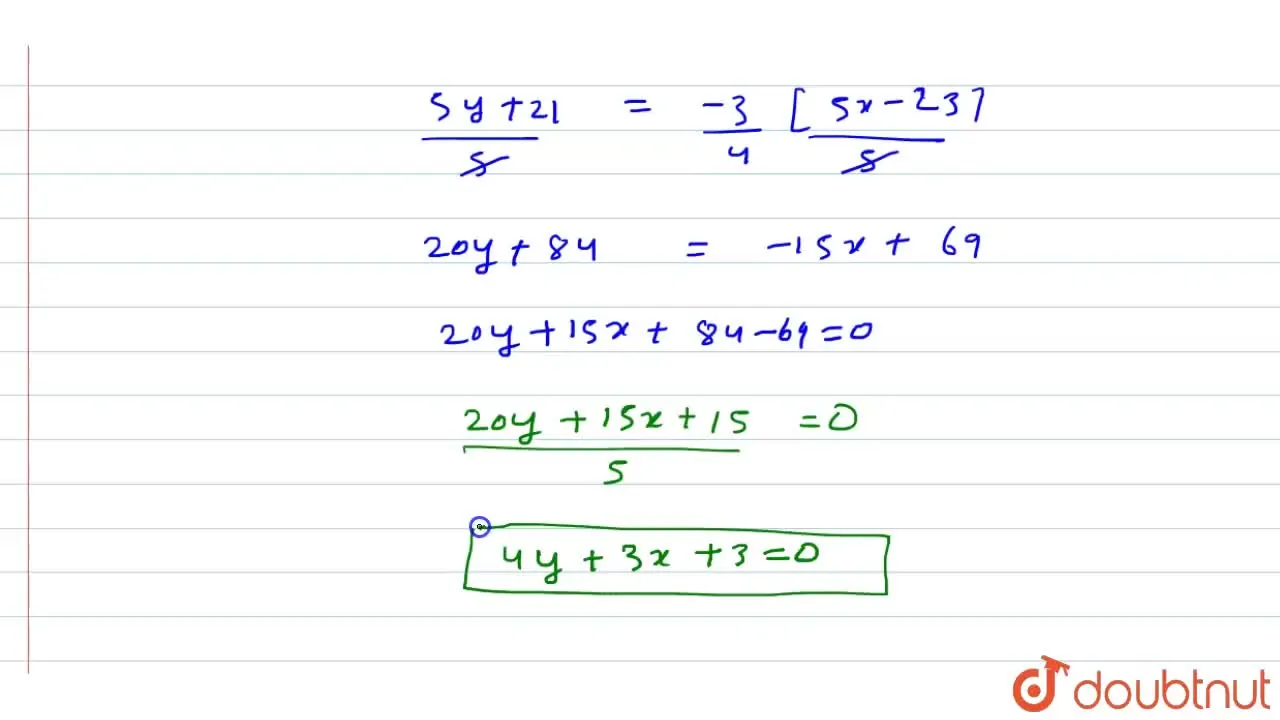Find the equation of the line passing through the intersection of the lines and parallel to the line
Step by step video & image solution for Find the equation of the line passing through the intersection of the lines 2x+y=5\ a n d\ x+3y+8=0 and parallel to the line 3x+4y=7. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
Similar Questions
Find the equation of a line passing through the intersection of the lines 3x−y=1 and 5x+2y=9 and parallel to the line 3x+5y=8.
View SolutionFind the equation of the straight line passing through the intersection of the lines x−2y=1 and x+3y=2 and parallel to 3x+4y=0.
View SolutionFind the equation of the straight line passing through the intersection of the lines x−2y=1 and x+3y=2 and parallel to 3x+4y=0.
View SolutionFind the equation of the line passing through the point of intersection of the lines x+5y+7=0 and 3x+2y−5=0
(a) parallel to the line 7x+2y−5=0View SolutionFind the equation of a line passing through the point of intersection of the lines x+3y+1=0 and 2x−y+3=0 and parallel to the line 3x−2y+1=0.
View SolutionFind the equation of a line which passes through the intersection of the lines 3x+y−2=0 and x−y+1=0 and parallel to Y-axis.
View SolutionFind the equation of a line which passes through the intersection of lines 2x+y−1=0 and x−3y+1=0 and parallel to x-axis.
View SolutionFind the equation of a line passing through the point of intersection of the lines x+y=4 and 2x−3y−1=0 and parallel to a line whose intercepts on the axes are 4 and 6 units.
View SolutionFind the equation of the straight line passing through the point of intersection of the two line x+2y+3=0and3x+4y+7=0 and parallel to the straight line y−x=8
View SolutionFind the equation of a line passing through the intersection of the lines x+3y=4 and 2x−y=1 and (0,0) lies on this line.
View Solution