In figure, is a parallelogram in which . Prove that .
To prove that the area of triangle PQE is equal to the area of triangle CFD, we can follow these steps:
1. Identify the Given Information:
We have a parallelogram PSDA where PQ=QR=RS and AP∥BQ∥CR∥DS.
Hint: Write down all the properties of the parallelogram and the relationships between the segments.
2. Establish Parallel Lines:
Since AP∥BQ∥CR∥DS, we can conclude that the segments BQ and CD are equal due to the properties of parallel lines.
Hint: Use the properties of parallel lines to establish relationships between the segments.
3. Identify Midpoints:
In triangle BED, point C is the midpoint of BD. Since CF∥BE, point F is the midpoint of ED.
Hint: Recall that the midpoints divide segments into equal parts.
4. Establish Equal Lengths:
From the midpoints, we can conclude that:
EF=FDandEF=PE
Therefore, we have:
PE=FD
Hint: Use the properties of midpoints to show that segments are equal.
5. Use Congruence Criteria:
In triangles PQE and CFD:
- We have PE=FD (from step 4).
- We have PQ=CD (from step 2, due to alternate angles).
Since we have two pairs of equal sides and the included angle is the same (as they are both between the parallel lines), we can use the Side-Angle-Side (SAS) congruence criterion to conclude that:
△PQE≅△CFD
Hint: Remember the congruence criteria for triangles to establish equality.
6. Conclude Areas are Equal:
Since the triangles PQE and CFD are congruent, their areas must also be equal:
Area(△PQE)=Area(△CFD)
Hint: Use the property of congruent triangles to conclude that their areas are equal.
Final Conclusion:
Thus, we have proved that:
Area(△PQE)=Area(△CFD)
Hence, the statement is proved.
We have a parallelogram PSDA where PQ=QR=RS and AP∥BQ∥CR∥DS.
Since AP∥BQ∥CR∥DS, we can conclude that the segments BQ and CD are equal due to the properties of parallel lines.
In triangle BED, point C is the midpoint of BD. Since CF∥BE, point F is the midpoint of ED.
From the midpoints, we can conclude that:
EF=FDandEF=PE
Therefore, we have:
PE=FD
In triangles PQE and CFD:
- We have PE=FD (from step 4).
- We have PQ=CD (from step 2, due to alternate angles).
△PQE≅△CFD
Since the triangles PQE and CFD are congruent, their areas must also be equal:
Area(△PQE)=Area(△CFD)
Thus, we have proved that:
Area(△PQE)=Area(△CFD)
Hence, the statement is proved.
Topper's Solved these Questions
Similar Questions
In Figure, AP||BQ ||CR. Prove that ar (AQC)= ar (PBR)
View SolutionIn △ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (△PBQ)= ar (△ ARC)
View SolutionIn △ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (△ PRQ)=12ar (△ ARC).
View SolutionIn △ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (△RQC)=38 ar (△ ABC).
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R, prove that R is a mid-point of BC.
View SolutionIn Figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that : ar(∣∣gmPQRS)=ar(∣∣gmABRS), ar(△AXS)=12ar(∣∣gmPQRS)
View SolutionIn Figure, ABCD and AEFD are two parallelograms? Prove that: ar ( APE): ar ( PFA)= ar (QFD) :ar ( PFD)
View SolutionIn Figure, If PQ=PT and ∠TPS=∠QPR, prove that PRS is isosceles
View SolutionIn Figure, ABCD is a parallelogram. Prove that: ar(BCP)=ar(DPQ) CONSTRUCTION : Join AC.
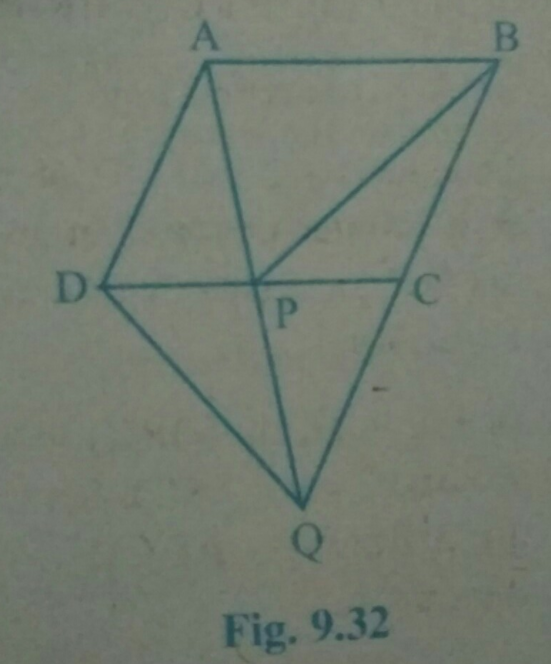
View SolutionIn Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such thatAD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).
View Solution

