In Figure, PQRS is a cyclic quadrilateral. Find the measure of each of its angles.
To find the measure of each angle in the cyclic quadrilateral PQRS, we can use the property that the opposite angles of a cyclic quadrilateral are supplementary. This means that the sum of the measures of opposite angles is 180∘.
Let's denote the angles as follows:
- ∠P=3x
- ∠Q=5y
- ∠R=x
- ∠S=y
Step 1: Set up the equations using the supplementary property
From the property of cyclic quadrilaterals, we can set up the following equations:
1. ∠P+∠R=180∘
3x+x=180∘
This simplifies to:
4x=180∘
2. ∠Q+∠S=180∘
5y+y=180∘
This simplifies to:
6y=180∘
Step 2: Solve for x and y
Now, we can solve for x and y from the equations we set up.
For x:
4x=180∘⟹x=180∘4=45∘
For y:
6y=180∘⟹y=180∘6=30∘
Step 3: Calculate each angle
Now that we have the values of x and y, we can find the measures of each angle:
- ∠P=3x=3×45∘=135∘
- ∠R=x=45∘
- ∠Q=5y=5×30∘=150∘
- ∠S=y=30∘
Summary of angles:
- ∠P=135∘
- ∠Q=150∘
- ∠R=45∘
- ∠S=30∘
- ∠P=3x
- ∠Q=5y
- ∠R=x
- ∠S=y
From the property of cyclic quadrilaterals, we can set up the following equations:
1. ∠P+∠R=180∘
3x+x=180∘
This simplifies to:
4x=180∘
5y+y=180∘
This simplifies to:
6y=180∘
Now, we can solve for x and y from the equations we set up.
4x=180∘⟹x=180∘4=45∘
6y=180∘⟹y=180∘6=30∘
Now that we have the values of x and y, we can find the measures of each angle:
- ∠R=x=45∘
- ∠Q=5y=5×30∘=150∘
- ∠S=y=30∘
- ∠P=135∘
- ∠Q=150∘
- ∠R=45∘
- ∠S=30∘
Topper's Solved these Questions
Similar Questions
In Figure, ABCD is a cyclic quadrilateral. Find the value of a and b.
View SolutionIn Figure, ABCD is a cyclic quadrilateral; O is the centre of the circle. If ∠BOD=1600, find the measure of ∠BPD
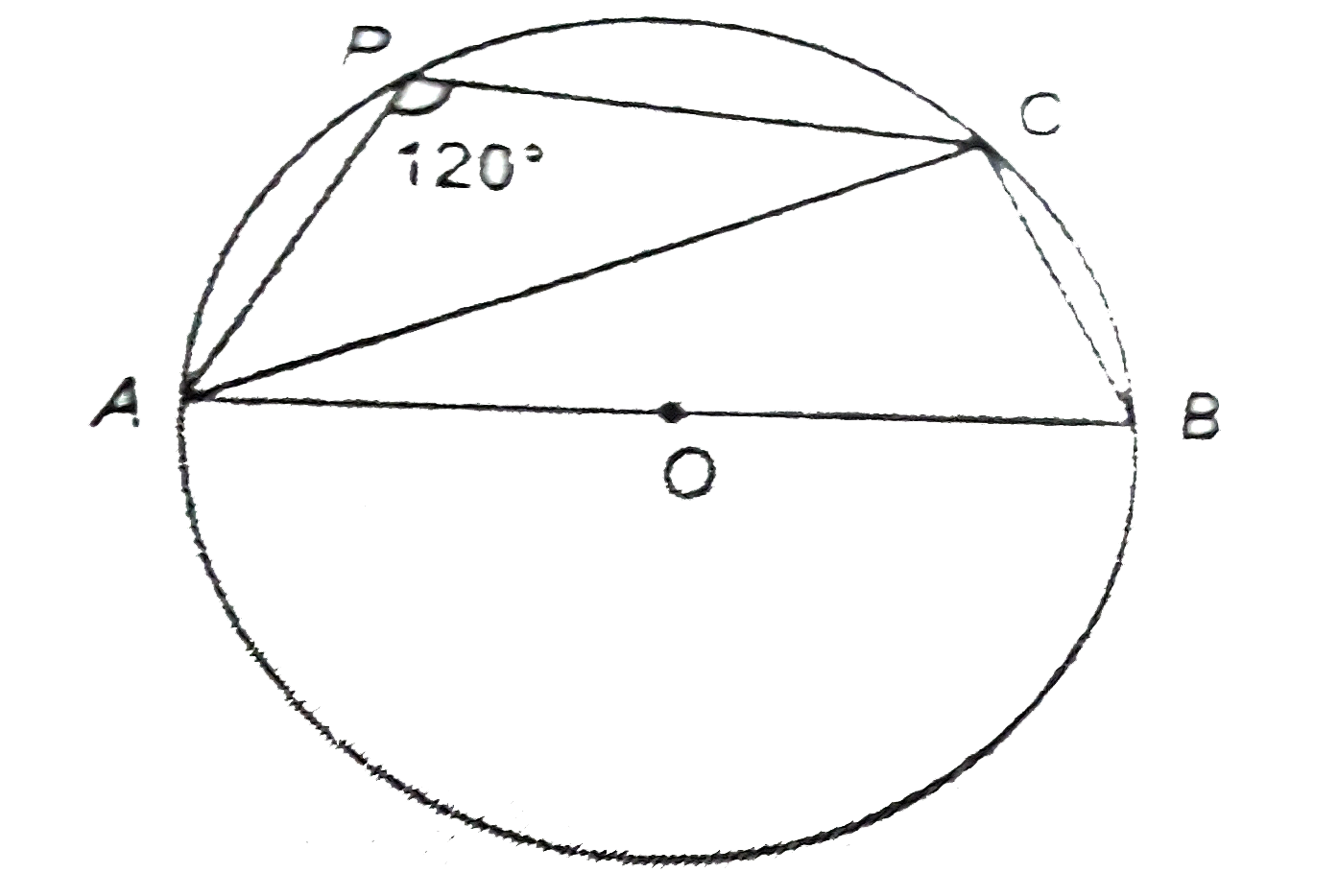
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠APC=120∘, then find the value of ∠CAB.
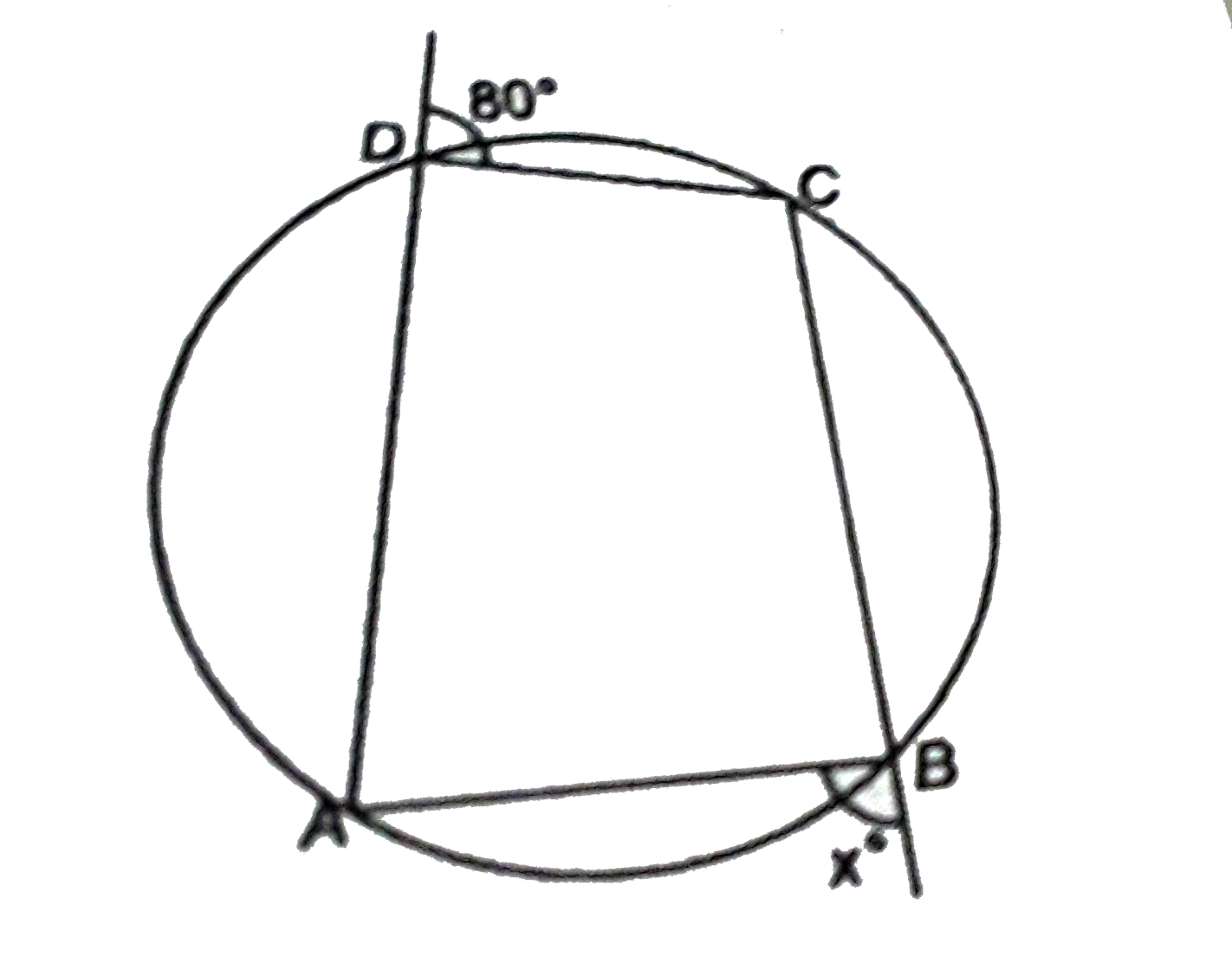
View SolutionIn the adjoining figure, if ABCD is a cyclic quadrilateral, find the value of x.
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If ∠ADC=140∘ , then find the value of ∠BAC.

View SolutionIn cyclic quadrilateral ABCD,∠A=3∠C and ∠D=5∠B. Find the measure of each angle of the quadrilateral.
View SolutionIn Figure, PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. Prove that ∠R> ∠P and ∠S> ∠Q.
View SolutionIn Figure, PQRS is a quadrilateral in which diagonals PR and QS intersect in O . Show that PQ+QR+RS+SP>PR+QS PQ+QR+RS+SP<2 (PR+QS) Figure
View SolutionIn Figure, PQRS is a quadrilateral and T and U are respectively points on PS and RS such that PQ=RQ, ∠PQT=∠RQU and ∠TQS=∠UQS. Prove that QT=QU.
View SolutionIf PQRS is a square, then write the measure of ∠SRP
View Solution
