In the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If ∠ADC=140∘ , then find the value of ∠BAC.

Since, ABCD is a cyclic quadrilateral .
∴∠ADC+∠ABC=180∘
⇒140∘+∠ABC=180∘
⇒∠ABC=180∘−140∘
⇒∠ABC=40∘
AB is the diameter of circle.
∴∠ACB=90∘ (angle in a semi- circle)
Now, in ΔABC
∠BAC=∠ABC+anl≥ACB=180∘
⇒∠BAC+40∘+90∘=180∘
⇒∠BAC=180∘−130∘
⇒∠BAC−50∘
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
In the adjoining figure, ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠APC=120∘, then find the value of ∠CAB.
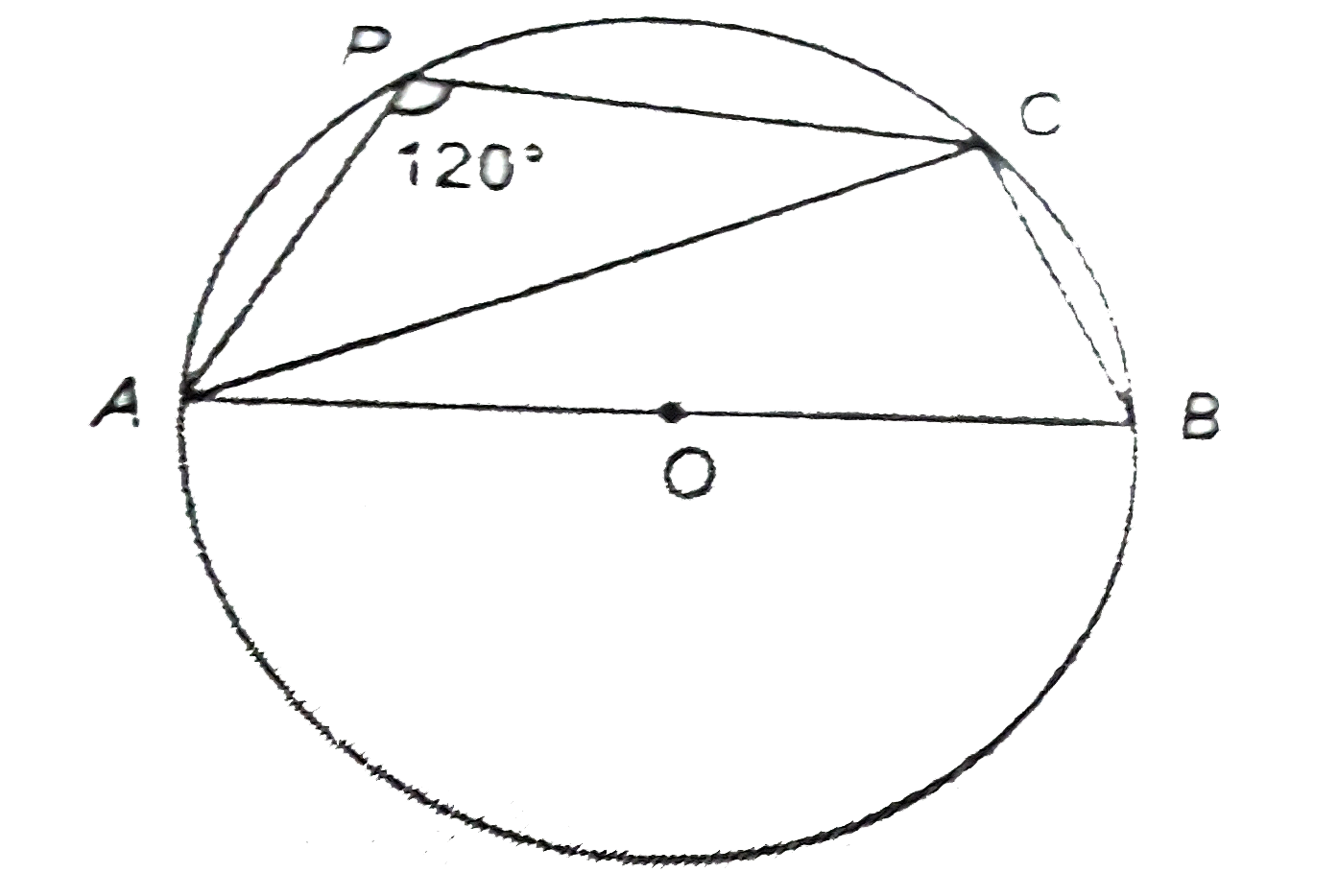
View SolutionIn the adjoining figure, if ABCD is a cyclic quadrilateral, find the value of x.
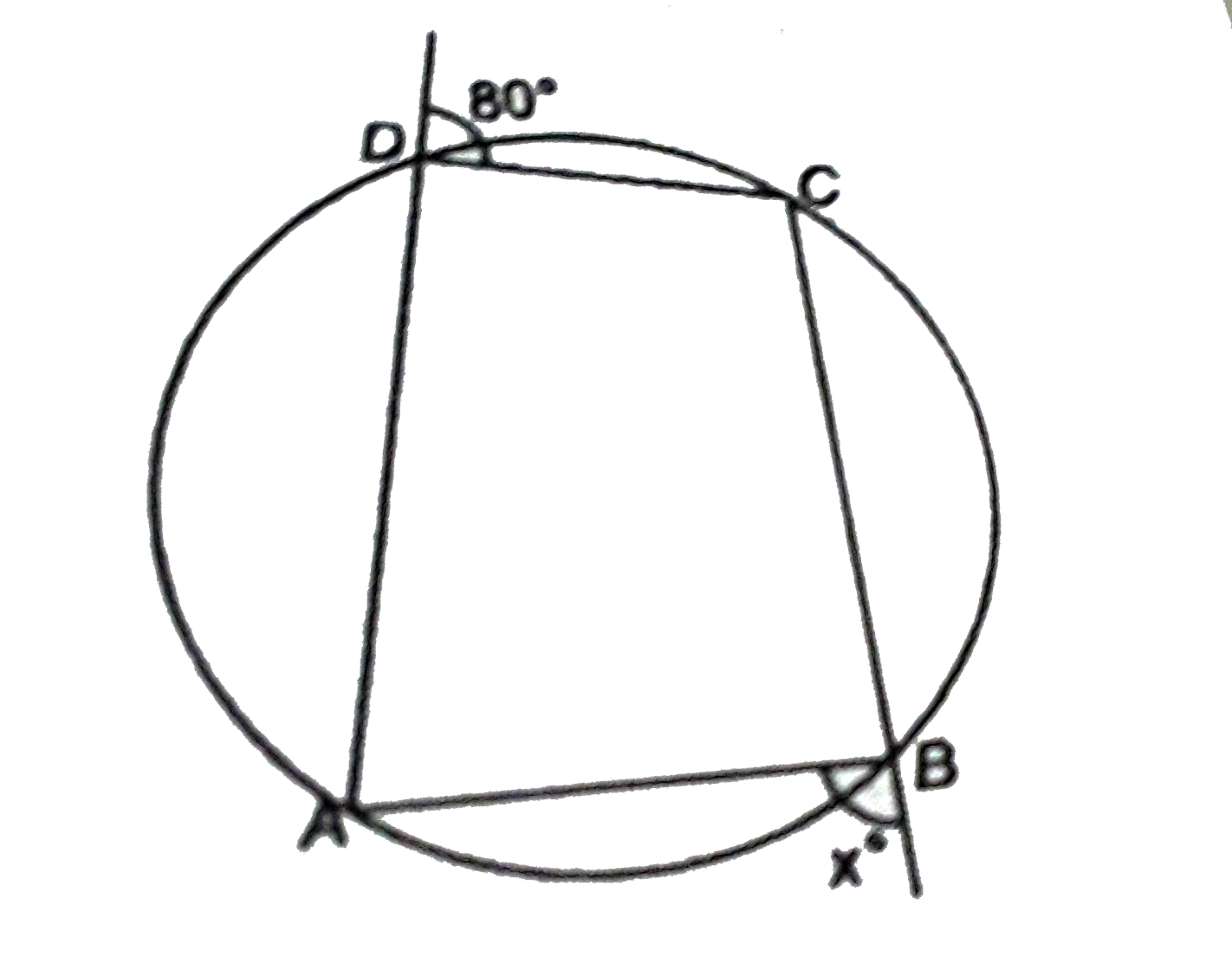
View SolutionIn the adjoining figure, AC is the diameter of the circle. If ∠BDC=115∘, then find the value of ∠ACB.
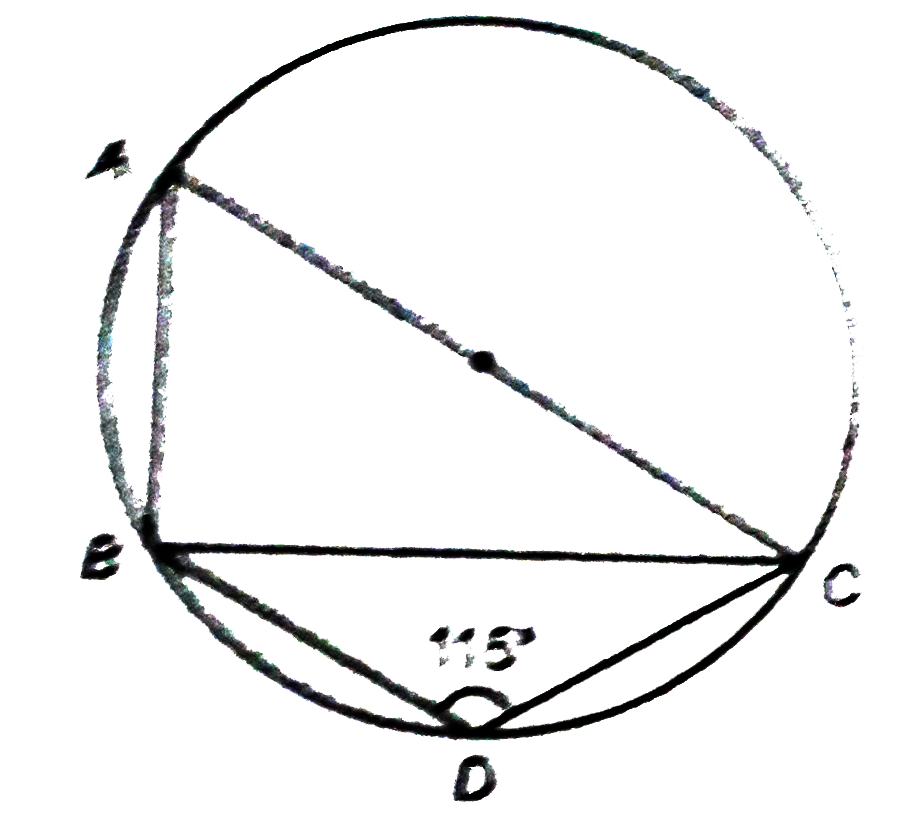
View SolutionIn the adjoining figure, AOB is the diameter of the circle. If ∠ABP=45∘, then find the value of ∠PQB.

View SolutionIn the adjoining figure, O is the centre of the circle.If ∠BAC=40∘, then find the value of ∠ADC.

View SolutionIn the adjoining figure,O is the centre of the circle. If ∠ABC=110∘ , then find the value of ∠AOC.
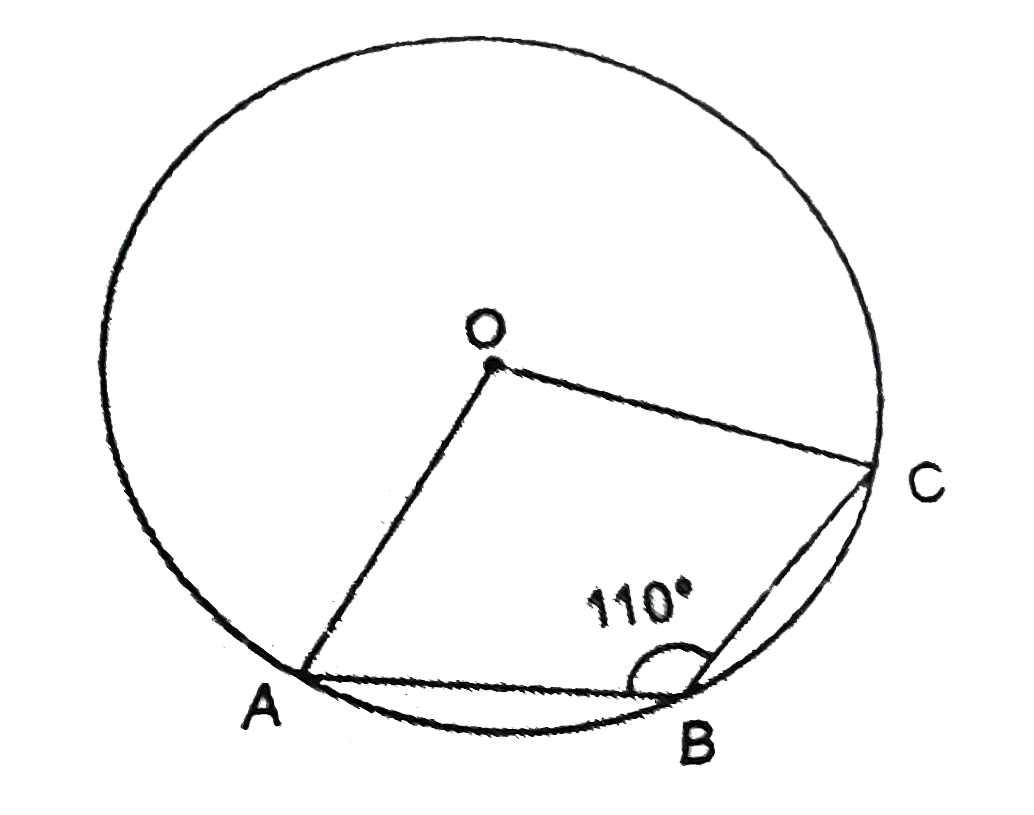
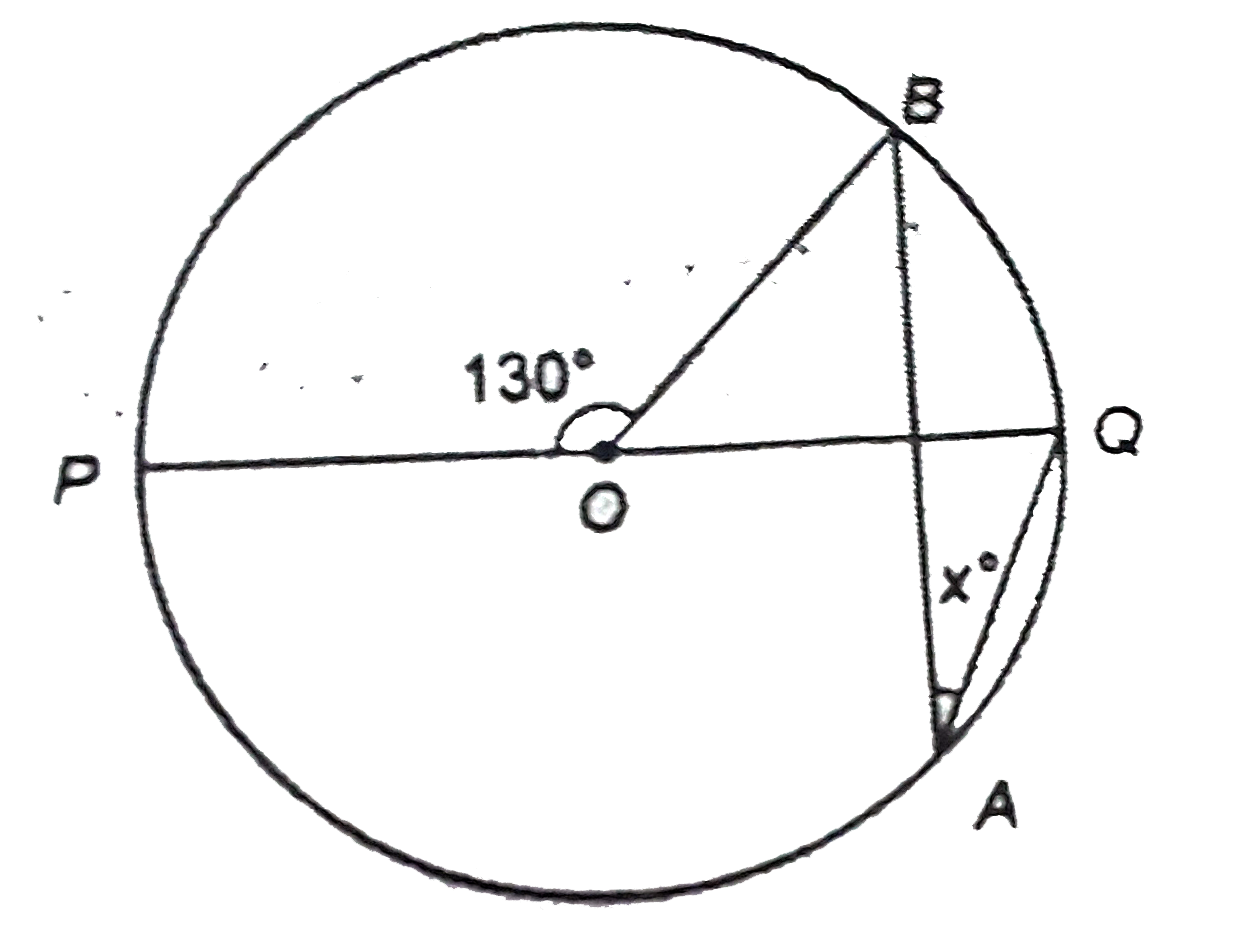
View SolutionIn the adjoining figure, O is the centre of the circle. If ∠BOP=130∘, then find the value of x.
View SolutionIn the adjoining figure, AD is the diameter of the circle and ∠BCD=140∘. Find the value of ∠ADB.

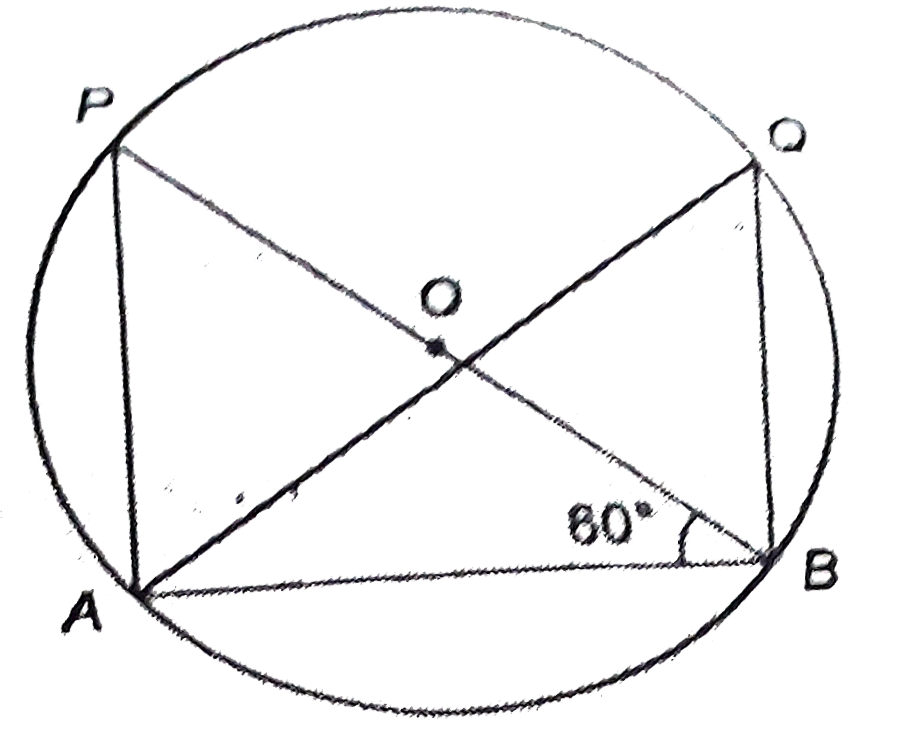
View SolutionIn the adjoining figure, BP is the diameter of the circle. If ∠ABP=60∘, then find ∠AQB.
View SolutionIn the adjoining figure, O is the centre of the circle. If ∠AOB=70∘, then find the value of ∠OCD.

View Solution
