After striking a floor a certain ball rebounds (45)th of the height from which it has fallen. Find the total distance that it travels before coming to rest, if it is gently dropped from a height of 120 metres.
To solve the problem of finding the total distance a ball travels after being dropped from a height of 120 meters and rebounding to 45 of the height from which it fell, we can follow these steps:
1. Initial Drop:
The ball is dropped from a height of 120 meters. This is the first distance traveled.
Distance1=120 meters
2. First Rebound:
After hitting the ground, the ball rebounds to 45 of the height it fell from.
Rebound Height1=45×120=96 meters
3. First Drop After Rebound:
The ball then falls again from this rebound height of 96 meters.
Distance2=96 meters
4. Second Rebound:
The ball rebounds again to 45 of 96 meters.
Rebound Height2=45×96=76.8 meters
5. Second Drop After Rebound:
The ball falls again from this height of 76.8 meters.
Distance3=76.8 meters
6. Continuing the Pattern:
This process continues indefinitely. The heights of the rebounds form a geometric progression (GP) where:
- First term a=120 (the initial drop)
- The subsequent terms are 2×(45)n×120 for n=0,1,2,…
7. Sum of the Distances:
The total distance traveled by the ball can be expressed as:
Total Distance=120+2(96+76.8+…)
The series 96,76.8,… is a GP with:
- First term a=96
- Common ratio r=45
8. Sum of the Infinite GP:
The sum S of an infinite GP is given by:
S=a1−r
For our series:
S=961−45=9615=96×5=480 meters
9. Total Distance Calculation:
Now substituting back into the total distance:
Total Distance=120+2×480=120+960=1080 meters
Final Answer:
The total distance that the ball travels before coming to rest is 1080 meters.
The ball is dropped from a height of 120 meters. This is the first distance traveled.
Distance1=120 meters
After hitting the ground, the ball rebounds to 45 of the height it fell from.
Rebound Height1=45×120=96 meters
The ball then falls again from this rebound height of 96 meters.
Distance2=96 meters
The ball rebounds again to 45 of 96 meters.
Rebound Height2=45×96=76.8 meters
The ball falls again from this height of 76.8 meters.
Distance3=76.8 meters
This process continues indefinitely. The heights of the rebounds form a geometric progression (GP) where:
- First term a=120 (the initial drop)
- The subsequent terms are 2×(45)n×120 for n=0,1,2,…
The total distance traveled by the ball can be expressed as:
Total Distance=120+2(96+76.8+…)
The series 96,76.8,… is a GP with:
- First term a=96
- Common ratio r=45
The sum S of an infinite GP is given by:
S=a1−r
For our series:
S=961−45=9615=96×5=480 meters
Now substituting back into the total distance:
Total Distance=120+2×480=120+960=1080 meters
The total distance that the ball travels before coming to rest is 1080 meters.
Topper's Solved these Questions
Similar Questions
After striking a floor a certain ball rebounds (45)th of the height from which it has fallen. Find the total distance that it travels before coming to rest, if it is gently dropped from a height of 120metres.
View SolutionAfter striking the floor, a certain ball rebounds (4/5)th of height from which it has fallen. Then the total distance that it travels before coming to rest, if it is gently dropped of a height of 120 m is a. 1260m b. 600m c. 1080m d. none of these
View Solution
Knowledge Check
A ball is dropped on to a horizontal plate from a height h = 9 m above it. If the coefficient of restitution is e=1/2, the total distance travelled before the ball comes to rest is
A10 mB15 mC20 mD25 m
A golf ball is dropped from a height of 80 m. Each time the ball hits the ground, it rebounds to 1/3 of the height through which it has fallen. Then total distance travelled by the ball is 240m b. 160m c. 120m d. 320m
View SolutionA partical falls from a height h upon a fixed horizontal plane and rebounds. If e is the coefficient of restitution, the total distance travelled before rebounding has stopped is
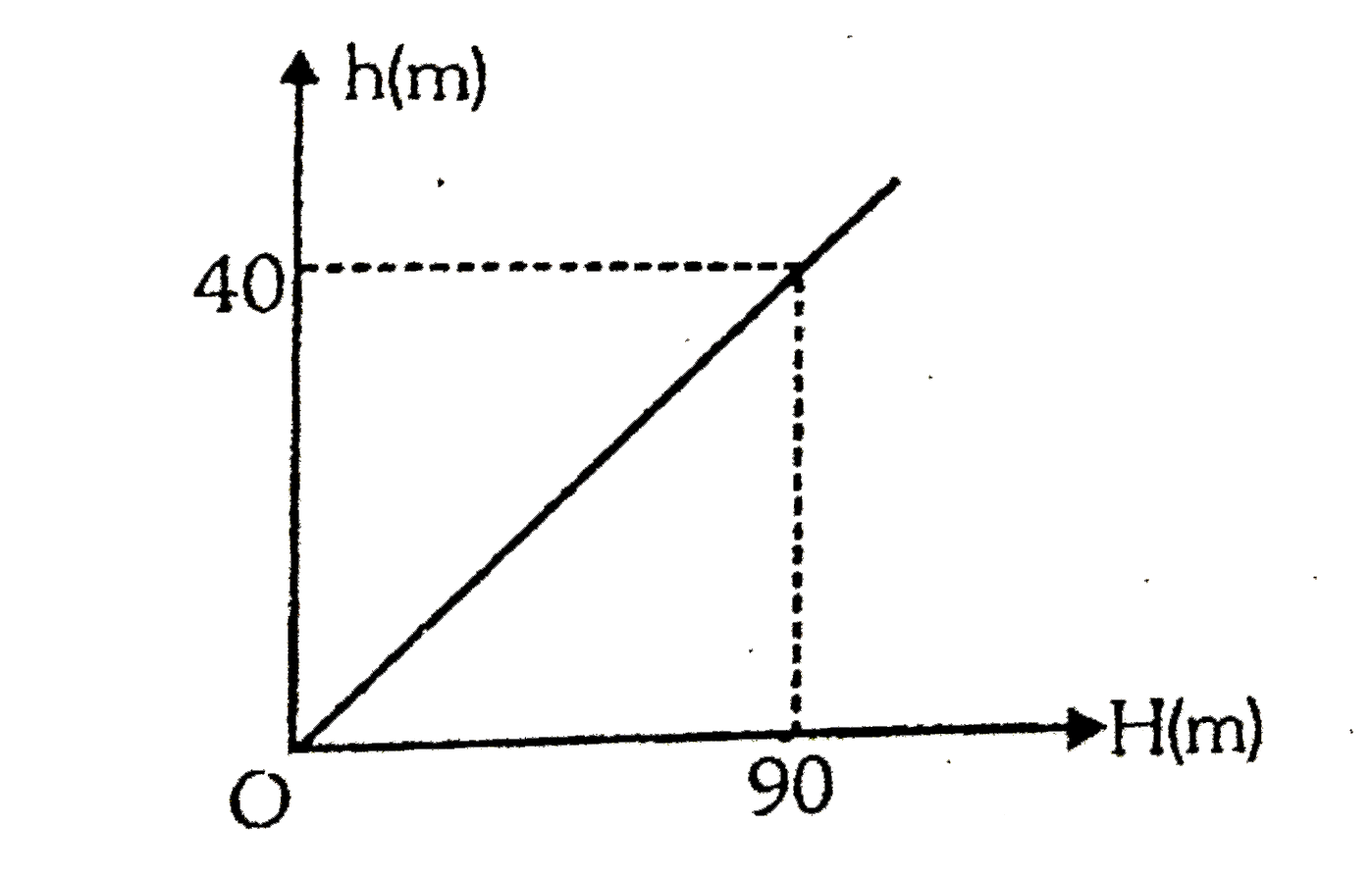
View SolutionA ball of mass 2kg dropped from a height H above a horizontal surface rebounds to a height h after one bounce. The graph that relates H to h is shown in figure. If the ball was dropped from an initial height of 81 m and made ten bounces, the kinetic energy of the ball immediately after the second impact with the surface was
View SolutionA ball is dropped from a height of 5 m onto a sandy floor and penetrates the sand up to 10 cm before coming to rest. Find the retardation of the ball in and assuming it to be uniform.
View SolutionA particle is dropped from top of tower. During its motion it covers 925 part of height of tower in last 1 sec. Then find height of the tower.
View SolutionA ball is dropped on a floor from a height h. If the coefficient of restitution is e, find the height to which the ball will rise after touching the floor and the time it will take to come to rest again.
View SolutionA ball is released from some height & rebounds with same speed after hitting the ground.If it travels 20m in first 8 seconds find the no of collision made.
View Solution