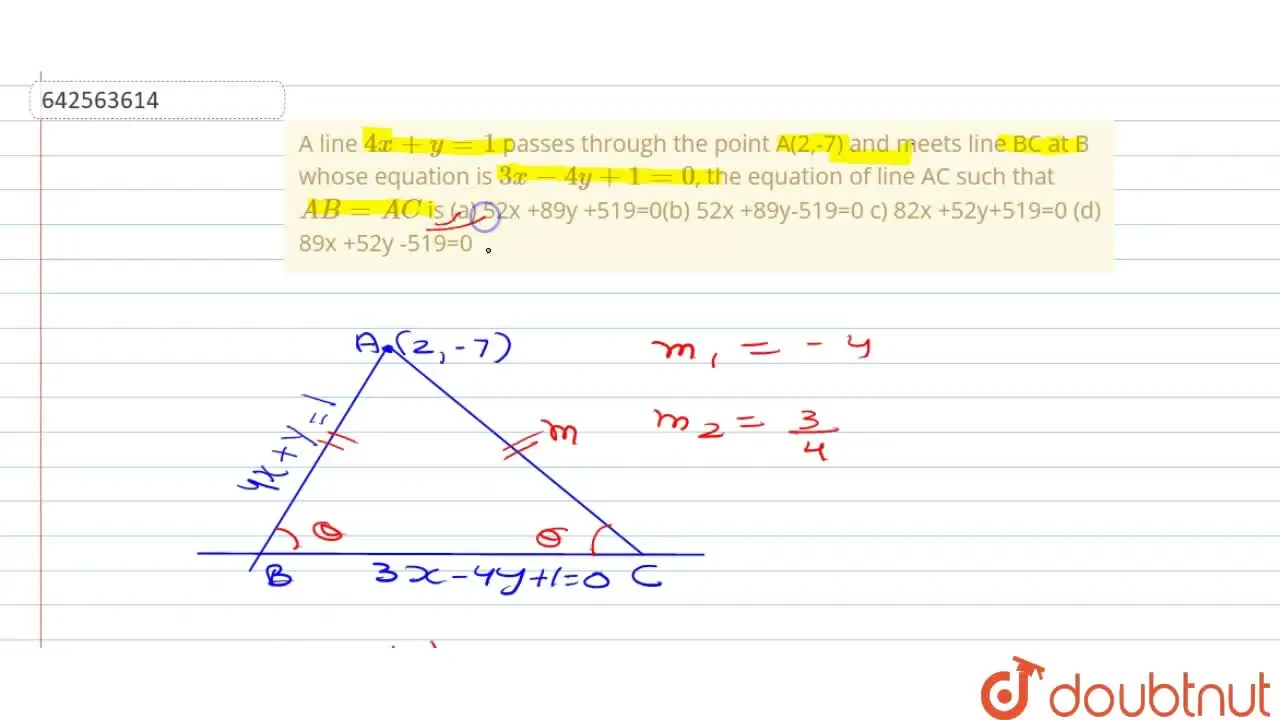
A line 4x+y=1 passes through the point A(2,-7) and meets line BC at B whose equation is 3x−4y+1=0, the equation of line AC such that AB=AC is (a) 52x +89y +519=0(b) 52x +89y-519=0 c) 82x +52y+519=0 (d) 89x +52y -519=0
Step by step video & image solution for A line 4x+y=1 passes through the point A(2,-7) and meets line BC at B whose equation is 3x -4y +1=0, the equation of line AC such that AB=AC is (a) 52x +89y +519=0(b) 52x +89y-519=0 c) 82x +52y+519=0 (d) 89x +52y -519=0 by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
Similar Questions
Find the equation of a line passing through the point (2,3) and parallel to the line 3x−4y+5=0 .
View SolutionEquation of line touching both parabolas y2=4x and x2=−32y is a) x+2y + 4 =0 b) 2x +y4 =0 c) x-2y-4 =0 d) x-2y+4 =0
View SolutionFind the lines whose combined equation is 6x2+5xy−4y2+7x+13y−3=0
View SolutionFind the lines whose combined equation is 6x2+5xy−4y2+7x+13y−3=0
View SolutionA straight line through the point A (−2,−3) cuts the line x+3y=9 and x+y+1=0 at B and C respectively. If AB.AC=20 then equation of the possible line is
View SolutionDetermine the angle between the lines whose equation are
3x+y−7=0andx+2y+9=0,View SolutionA ray of light is incident along a line which meets another line, 7x−y+1=0, at the point (0, 1). The ray isthen reflected from this point along the line, y+2x=1. Then the equation of the line of incidence of the ray of light is (A) 41x+38y−38=0 (B) 41x−38y+38=0 (C) 41x+25y−25=0 (D) 41x−25y+25=0
View SolutionProve that the line y−x+2 =0 divides the join of points (3,-1) and (8,9) in the ratio 2:3.
View SolutionGiven ABCD is a parallelogram with vertices as A(1,2),B(3,4) and C(2,3). Then the equation of line AD is (A) x+y+1=0 (B) x−y+1=0 (C) −x+y+1=0 (D) x+y−1=0
View SolutionA line passes through (−3,4) and the portion of the line intercepted between the coordinate axes is bisected at the point then equation of line is (A) 4x−3y+24=0 (B) x−y−7=0 (C) 3x−4y+25=0 (D) 3x−4y+24=0
View Solution