Given P(x)=x4+ax3+bx2+cx+d such that x=0 is the only real root of P'(x)=0. If P(−1)<P(1), then in the interval [−1,1]
(a) P(-1) is the minimum and P(1) is the maximum of P
(b) P(-1) is not minimum but P(1) is the maximum of P
(c) P(-1) is not minimum and P(1) is not the maximum of P
(d) neither P(-1) is the minimum nor P(1) is the maximum of P
The correct Answer is:2
P(x)=x4+ax3+bx2+cx+d
P(x)=4x3+3ax2+2bx+c
Since x=0 is solution to P(x) =0 we get c=0 Therefore
P(x)=x4+ax3+bx2+d
Also we have
P(−1)<P(1)
→1−a+b+d<1+a+b+d→a>0
Since P(x) =0 only when x=0 and P(x) is differentiable in
(-1,1) we should have the maximum and minimum points x=-1,0 and 1 only
Also we have f(-1)<P(1)
Maximum of P(x) =maximum {P(0),P(1)}and
Minimum of f(x)=minimum {P(-21),P(0)}
In the interval [0,1]
P(x)=4x3+3ax2+2bx{(p(1)} and
4x2+3ax+2b=0 has no real roots .Therefore
(3a)2−32b<0
→9a232<b
→b>0
Thus we have a>0andbv>0 Thus
P(x) =4x3+3ax2+2bx>0∀x∈(0,1)
Hence P(x) is increasing in [0,1]
Similarly P(x) id P(1)
Therefore the minimum of P(x) does not occur at x=1
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Linked comprehension Type2videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Linked comprehension type50videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Numerical Value Type24videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
Similar Questions
Letf(x)=x4+ax3+bx2+cx+d be a polynomial with real coefficients and real roots. If |f(i)|=1where i=√−1, then the value of a +b+c+d is
View SolutionIf the roots of ax3+bx2+cx+d=0 are in G.P then the roots of dx3−cx2+bx−a=0 are in
View SolutionLet P(x)=x2+12x+b and Q(x)=x2+cx+d be two polynomials with real coefficients such that P(x)Q(x)=Q(P(x)) for all real x. Find all the real roots of P(Q(x)) =0.
View SolutionIf P(x)=ax2+bx+c, and Q(x)=−ax2+dx+c,ax≠0 then prove that P(x),Q(x)=0 has atleast two real roots.
View SolutionLet Pn(x)=1+2x+3x2+............+(n+1)xn be a polynomial such that n is even.The number of real roots of Pn(x)=0 is
View SolutionLet a,b,c∈R with a>0 such that the equation ax2+bcx+b3+c3−4abc=0 has non-real roots.
If P(x)=ax2+bx+candQ(x)=ax2+cx+b, then (a) P(x)>0 for all x∈R and Q(x)<0 for all x∈R. (b) P(x)<0 for all x∈RandQ(x)>0 for all x∈R. (c) neither P(x)>0 for all x∈R nor Q(x)>0 for all x∈R. (d) exactly one of P(x) or Q(x) is positive for all real x.View SolutionLet Pn(ix)=1+2x+3x2+............+(n+1)xn be a polynomial such that n is even.The number of real roots of Pn(x)=0 is
View SolutionLet Pn(ix)=1+2x+3x2+............+(n+1)xn be a polynomial such that n is even.The number of real roots of Pn(x)=0 is
View SolutionIn the given figure graph of y=p(x)=x4+ax3+bx2+cx+d is given
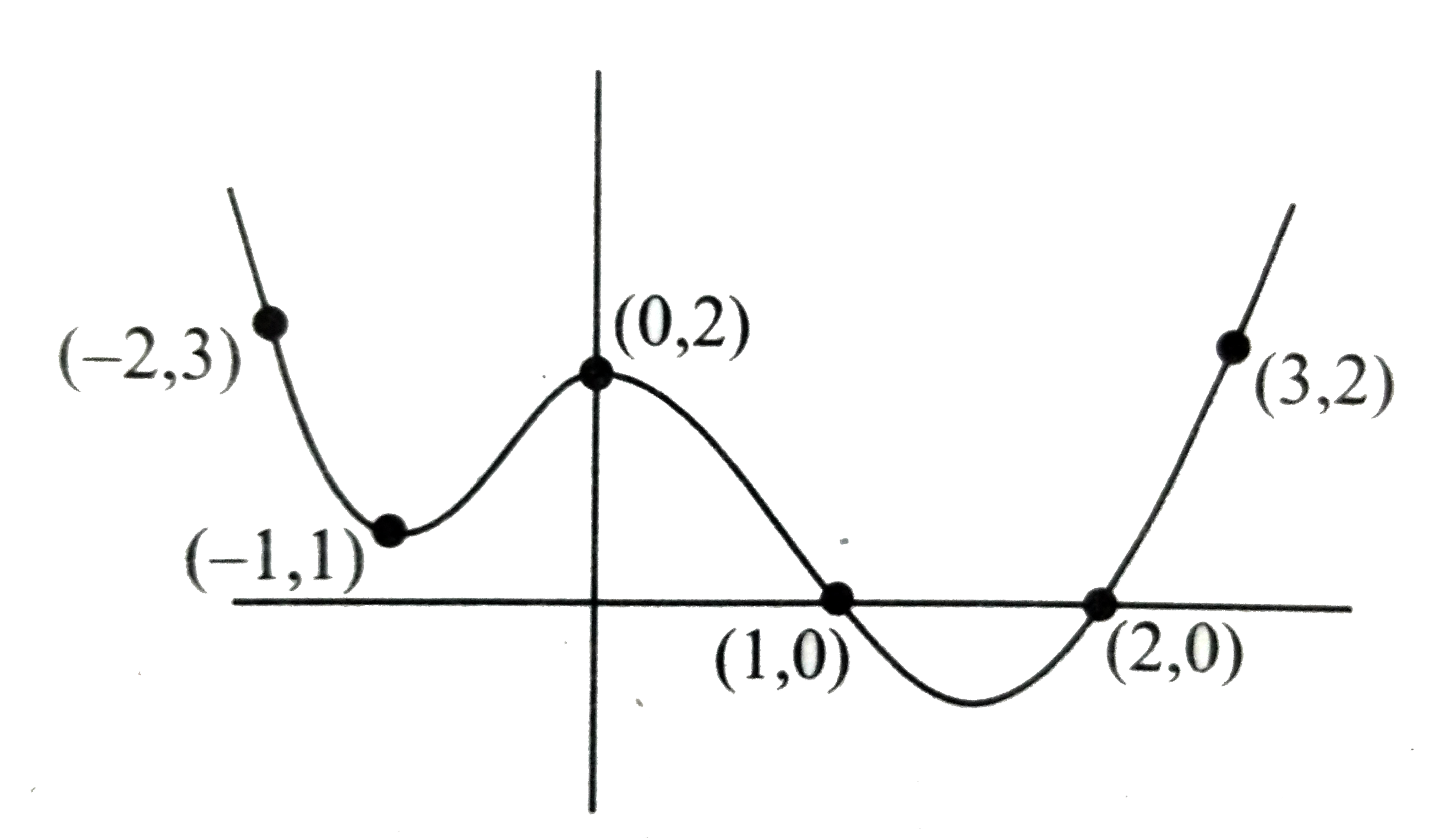
The product of all imaginary roots of p(x)=0 is (a) 1 (b) 2 (c) 13 (d) 14View SolutionLet f(x)=x3+x+1 and P(x) be a cubic polynomial such that P(0) = -1 and roots of f(0) = 1 ; P(x) = 0 are the squares of the roots of f(x) = 0 . Then find the value of P(4).
View Solution
