In the given figure graph of y=p(x)=x4+ax3+bx2+cx+d is given
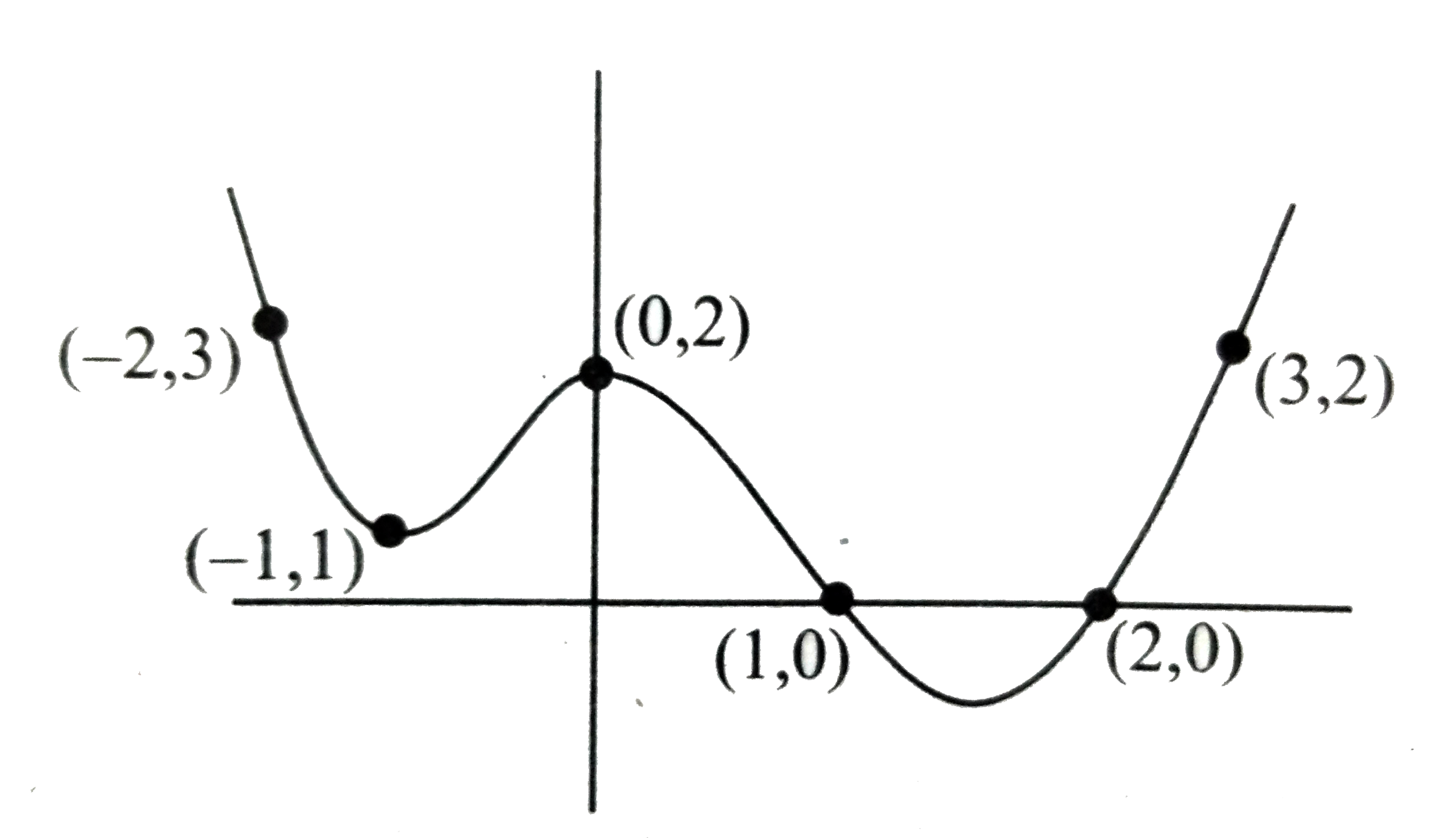
The product of all imaginary roots of p(x)=0 is
(a) 1
(b) 2
(c) 13
(d) 14
1
2
1/3
1/4
The correct Answer is:A
(a) 1.2(α+iβ)(α−iβ)=p(0)=2⇒(α+iβ)(α−iβ)=1
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Comprehension
12 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Multiple Correct Answer
6 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
294 Videos
Similar Questions
In the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.
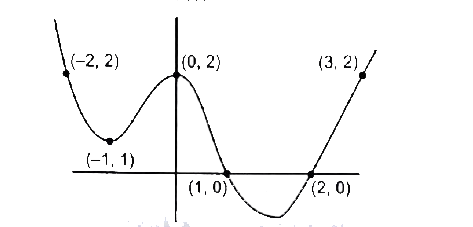
The product of all imaginary roots of p(x)=0 is:
View SolutionIn the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.
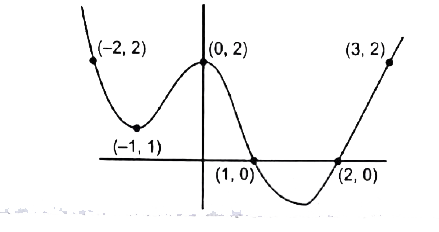
The minimum number of real roots of equation (p'(x))2+p(x)p''(x)=0 are:
View SolutionGiven P(x)=x4+ax3+bx2+cx+d such that x=0 is the only real root of P'(x)=0. If P(−1)<P(1), then in the interval [−1,1]
View SolutionIf (x−1)3 is a factor of x4+ax3+bx2+cx−1=0 then the other factor is
View SolutionIf the roots of ax3+bx2+cx+d=0 are in G.P then the roots of dx3−cx2+bx−a=0 are in
View SolutionIn Figure, the graph of a polynomial p(x) is shown. The number of zeroes of p(x) is (a)4 (b) 1 (c) 2 (d) 3
View SolutionIf the product of the roots of the equation 2x2+ax+4sina=0 is 1, then roots will be imaginary, if
View Solutionif x2+x+1 is a factor of ax3+bx2+cx+d then the real root of ax3+bx2+cx+d=0 is : (a) −da (B) da (C) ab (D)none of these
View SolutionFind the values of a,b,c,d, if 1,2,3,4 are the roots of x4+ax3+bx2+cx+d=0
View SolutionIf 1,2,3 are the roots of ax3+bx2+cx+d=0 then the roots of ax√x+bx+c√x+d=0 are
View Solution
