The number of nonzero integral values of a for which the function f(x)=x4+ax3+3x22+1 is concave upward along the entire real line is___________
The correct Answer is:4
To determine the number of nonzero integral values of a for which the function
f(x)=x4+ax3+3x22+1
is concave upward along the entire real line, we need to analyze the second derivative of the function.
Step 1: Find the first derivative f′(x)
The first derivative of f(x) is calculated as follows:
f′(x)=ddx(x4)+ddx(ax3)+ddx(3x22)+ddx(1)
Calculating each term gives:
f′(x)=4x3+3ax2+3x
Step 2: Find the second derivative f′′(x)
Now, we differentiate f′(x) to find f′′(x):
f′′(x)=ddx(4x3)+ddx(3ax2)+ddx(3x)
Calculating each term gives:
f′′(x)=12x2+6ax+3
Step 3: Set the condition for concavity
For the function to be concave upward along the entire real line, we need:
f′′(x)≥0for all x
This means that the quadratic 12x2+6ax+3 must not have any real roots, which occurs when its discriminant is less than or equal to zero.
Step 4: Calculate the discriminant
The discriminant D of the quadratic Ax2+Bx+C is given by:
D=B2−4AC
For our quadratic 12x2+6ax+3:
- A=12
- B=6a
- C=3
Thus, the discriminant is:
D=(6a)2−4⋅12⋅3
Calculating this gives:
D=36a2−144
Step 5: Set the discriminant less than or equal to zero
We need:
36a2−144≤0
This simplifies to:
36a2≤144
Dividing through by 36:
a2≤4
Taking the square root of both sides gives:
−2≤a≤2
Step 6: Identify nonzero integral values of a
The integral values of a that satisfy this inequality are:
−2,−1,1,2
The nonzero integral values are:
−2,−1,1,2
Conclusion
Thus, the number of nonzero integral values of a is:
4
- B=6a
- C=3
Topper's Solved these Questions
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Single Correct Answer Type
13 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Linked comprehension Type
2 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Multiple correct answers type
48 Videos
- METHODS OF DIFFERENTIATIONBOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type
46 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type
6 Videos
Similar Questions
Concavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)
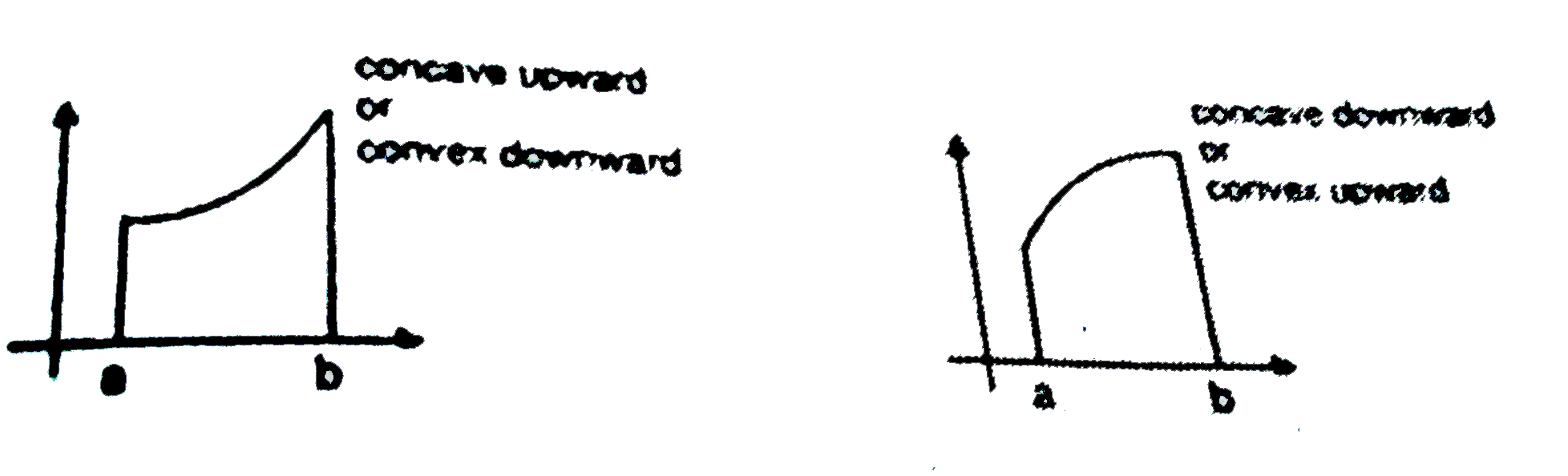
Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)

Exhaustive set of values of 'a' for which the function f(x)=x4+ax3+3x22+1 will be concave upward along the entire real line is : (A) [−1,1] (B) [−2,2] (C) [0,2] (D) [0,4]
View SolutionFind the values of x for which the functions f(x)=3x2−1 and g(x)=3+x are equal
View SolutionFind the values of x for which the functions f(x)=3x2−1 and g(x)=3+x are equal
View SolutionFind the values of x for which the functions f(x)=3x2−1 and g(x)=3+x are equal
View SolutionThe number of integral values in the range of the function f(x)=sin−1x−cot−1x+x2+2x+6 is
View SolutionNumber of integral values of x satisfying function f(x)=log(x−1)+log(3−x)
View SolutionFind the number of integral vaues of 'a' for which the range of function f(x)=x2−ax+1x2−3x+2is (−∞,∞),
View SolutionThe number of integral values of a for which f(x)=x3+(a+2)x2+3ax+5 is monotonic in ∀x∈R
View SolutionFind the values 'a' for which the function f(x)=(a+2)x3−3ax2+9ax−1 decreases for all real values of x .
View SolutionFind the values of a for which the function f(x)=(a+2)x3−3ax2+9ax−1 decreasing for all real values of x.
View Solution
