Three coinitial vectors of magnitudes a, 2a and 3a meet at a point and their directions are along the diagonals if three adjacent faces if a cube. Determined their resultant R. Also prove that the sum of the three vectors determinate by the diagonals of three adjacent faces of a cube passing through the same corner, the vectors being directed from the corner, is twice the vector determined by the diagonal of the cube.
Let the length of an edge of the cube be taken as unity and the vectors represented by OA, OB and OC (let the three coterminous edges of unit be ˆi,ˆjandˆk, respectively). OR, OS and OT are the three diagonals of the three adjacent faces of the cube along which act the forces of magnitudes a,2aand3a, respectively. To find the vectors representing these forces, we will first find unit vectors in these directions and then multiply them by the corresponding given magnitudes of these forces.
Since −−→OR=ˆj+ˆk, the unit vector along OR is 1√2(ˆj+ˆk).

Hence, force −→F1 of magnitude a along OR is given by
−→F1=a√2(ˆi+ˆk)
Similarly, force −→F1 of magnitude 2a along OS is 2a√2(ˆk+ˆi) and force −→F3 of magnitude 3a along OT is 3a√2(ˆi+ˆj).
If →R is their resultant, then
→R=−→F1+−→F2+−→F3
=a√2(ˆj+ˆk)+2a√2(ˆk+ˆi)+3a√2(ˆi+ˆj)
=5a√2ˆi+4a√2ˆj+3a√2ˆk
Again, −−→OR+−−→OS+−−→OT=ˆj+ˆk+ˆi+ˆk+ˆi+ˆj
=2(ˆi+ˆj+ˆk)
Also, −−→OP=−−→OT+−−→TP=(ˆi+ˆj+ˆk) (∵−−→OT=ˆi+ˆjand−−→TP=−−→OC=ˆk)
−−→OR+−−→OS+−−→OT=2−−→OP
Topper's Solved these Questions
- INTRODUCTION TO VECTORS Book:CENGAGE ENGLISHChapter:INTRODUCTION TO VECTORS Exercise:ILLUSTRATION 28
Explore 1 Video
- INTRODUCTION TO VECTORS Book:CENGAGE ENGLISHChapter:INTRODUCTION TO VECTORS Exercise:ILLUSTRATION 29
Explore 1 Video
- INTRODUCTION TO VECTORS Book:CENGAGE ENGLISHChapter:INTRODUCTION TO VECTORS Exercise:ILLUSTRATION 26
Explore 1 Video
- INTEGRALSBook:CENGAGE ENGLISHChapter:INTEGRALSExercise:All Questions
Explore 764 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBook:CENGAGE ENGLISHChapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:Archives (Numerical Value type)
Explore 2 Videos
Similar Questions
Three vectors of magnitude a,2a,3a meet in a point and their directions are along the diagonals of the adjacent faces of a cube. Determine their resultant.
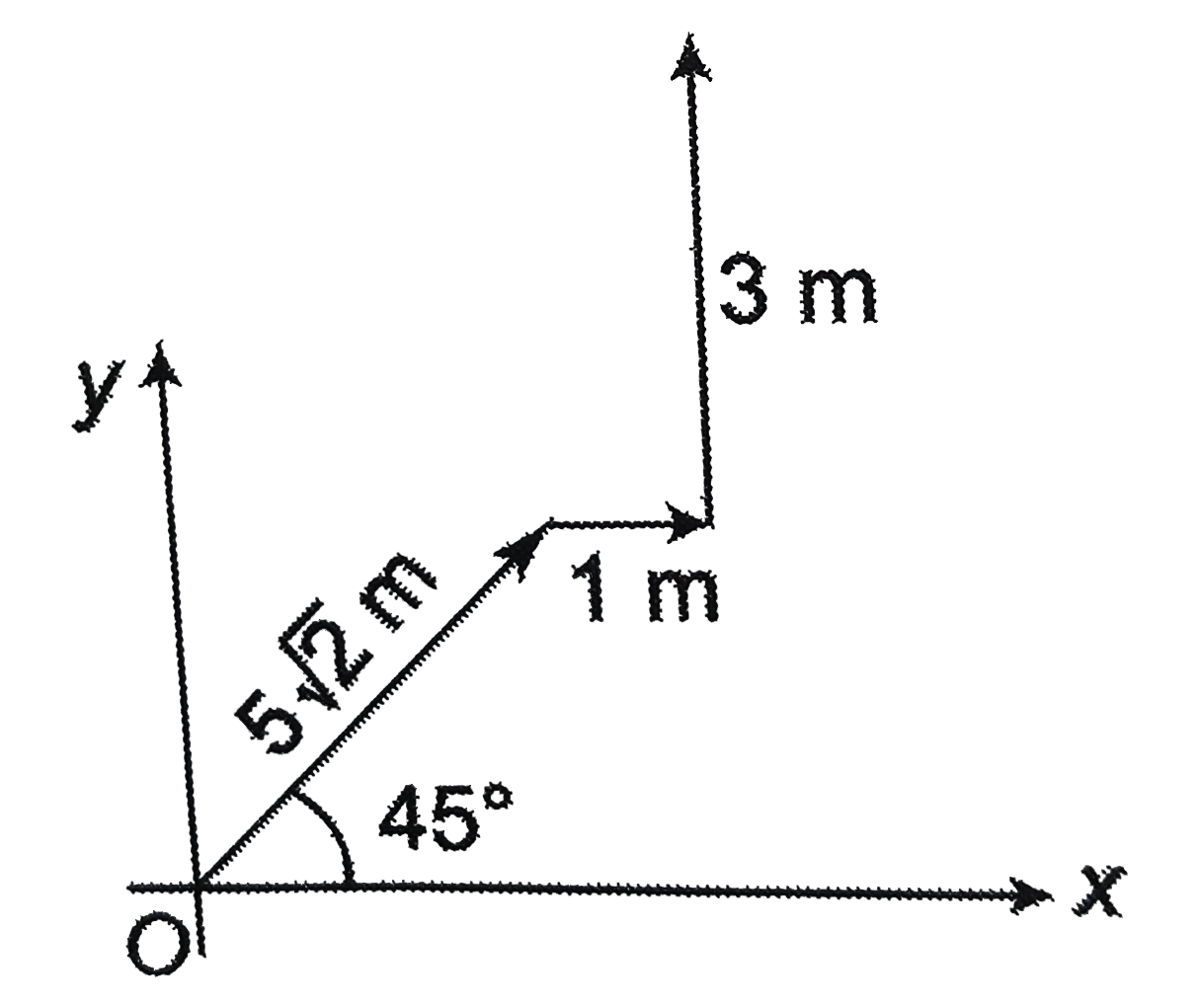
View SolutionThe sum of these three vectors is :
View SolutionProve that the sum of three vectors determined by the medians of a triangle directed from the vertices is zero.
View SolutionProve that the sum of three vectors determined by the medians of a triangle directed from the vertices is zero.
View SolutionShow that the sum of three vectors determined by the medians of a triangle directed from the vertices is zero.
View SolutionShow that the sum of three vectors determined by the medians of a triangle directed from the vertices is zero.
View SolutionThe areas of three adjacent faces of a cuboid are x, y and z. If the volume is V, prove that V2=xyz.
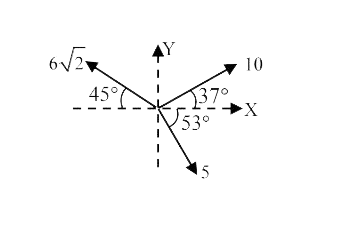
View SolutionFind the resultant of the three vectors shown in figure .
 .
.
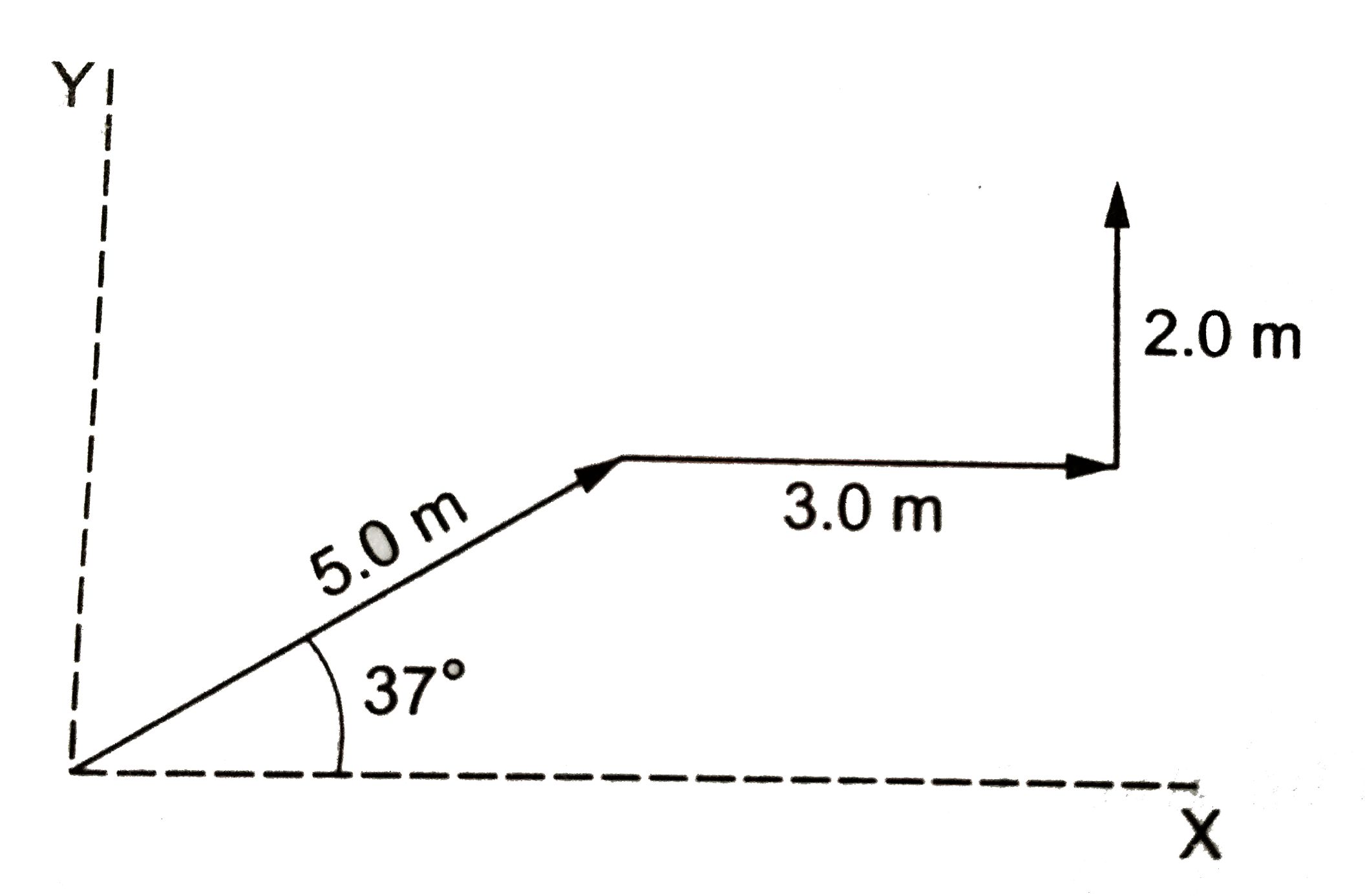
View SolutionFind the resultant of three vectors shown in the figure.
View SolutionThe angle between diagonal of a cube and diagonal
of a face of the cube will be
View Solution

