Prove that the sum of three vectors determined by the medians of a triangle directed from the vertices is zero.
To prove that the sum of the three vectors determined by the medians of a triangle directed from the vertices is zero, we can follow these steps:
Step 1: Define the Triangle and Medians
Let triangle ABC have vertices A, B, and C. The midpoints of the sides BC, CA, and AB are denoted as D, E, and F, respectively. The medians AD, BE, and CF are drawn from vertices A, B, and C to the midpoints D, E, and F.
Step 2: Express the Medians as Vectors
The vectors representing the medians can be expressed as:
- Median AD:
→AD=→B+→C2−→A=→B+→C−2→A2
- Median BE:
→BE=→C+→A2−→B=→C+→A−2→B2
- Median CF:
→CF=→A+→B2−→C=→A+→B−2→C2
Step 3: Sum the Medians
Now, we sum the three median vectors:
→AD+→BE+→CF=(→B+→C−2→A2)+(→C+→A−2→B2)+(→A+→B−2→C2)
Step 4: Combine the Terms
Combining the terms inside the parentheses:
=(→B+→C−2→A)+(→C+→A−2→B)+(→A+→B−2→C)2
=→B+→C−2→A+→C+→A−2→B+→A+→B−2→C2
Step 5: Simplify the Expression
Now, let's simplify the numerator:
=(1−2)→A+(1−2)→B+(1−2)→C2
=−→A−→B−→C2
This simplifies to:
=−→A−→B−→C2=0
Conclusion
Thus, we conclude that:
→AD+→BE+→CF=0
This proves that the sum of the three vectors determined by the medians of a triangle directed from the vertices is zero.
---
Let triangle ABC have vertices A, B, and C. The midpoints of the sides BC, CA, and AB are denoted as D, E, and F, respectively. The medians AD, BE, and CF are drawn from vertices A, B, and C to the midpoints D, E, and F.
The vectors representing the medians can be expressed as:
- Median AD:
→AD=→B+→C2−→A=→B+→C−2→A2
- Median BE:
→BE=→C+→A2−→B=→C+→A−2→B2
- Median CF:
→CF=→A+→B2−→C=→A+→B−2→C2
Now, we sum the three median vectors:
→AD+→BE+→CF=(→B+→C−2→A2)+(→C+→A−2→B2)+(→A+→B−2→C2)
Combining the terms inside the parentheses:
=(→B+→C−2→A)+(→C+→A−2→B)+(→A+→B−2→C)2
=→B+→C−2→A+→C+→A−2→B+→A+→B−2→C2
Now, let's simplify the numerator:
=(1−2)→A+(1−2)→B+(1−2)→C2
=−→A−→B−→C2
This simplifies to:
=−→A−→B−→C2=0
Thus, we conclude that:
→AD+→BE+→CF=0
This proves that the sum of the three vectors determined by the medians of a triangle directed from the vertices is zero.
Topper's Solved these Questions
Similar Questions
Show that the sum of three vectors determined by the medians of a triangle directed from the vertices is zero.
View SolutionShow that the sum of three vectors determined by the medians of a triangle directed from the vertices is zero.
View SolutionThe sum of these three vectors is :
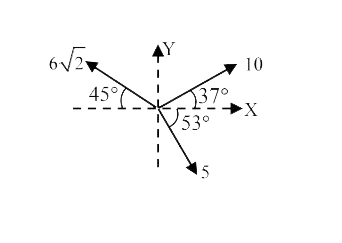
View SolutionThree coinitial vectors of magnitudes a, 2a and 3a meet at a point and their directions are along the diagonals if three adjacent faces if a cube. Determined their resultant R. Also prove that the sum of the three vectors determinate by the diagonals of three adjacent faces of a cube passing through the same corner, the vectors being directed from the corner, is twice the vector determined by the diagonal of the cube.
View SolutionProve that the medians of a triangle are concurrent.
View SolutionProve that the sum of all vectors drawn from the centre of a regular octagon to its vertices is the zero vector.
View SolutionProve that the sum of the three angles of a triangle is 1800.
View SolutionProve that three times the sum of the squares of the sides of a triangle is equal to four times the sum of the squares of the medians of the triangle.
View SolutionProve that the locus of the point that moves such that the sum of the squares of its distances from the three vertices of a triangle is constant is a circle.
View SolutionProve using vectors: If two medians of a triangle are equal, then it is isosceles.
View Solution

