In cyclic quadrilateral ABCD (none of these being 90∘), which of the following is not true ?
tan A cot C = -1
sec B cos D = -1
cosec B sin D = 1
none of these
The correct Answer is:D
To solve the problem regarding the cyclic quadrilateral ABCD and determine which of the statements is not true, we will analyze the properties of cyclic quadrilaterals and the relationships between their angles.
1. Understanding Cyclic Quadrilaterals:
A cyclic quadrilateral is a quadrilateral whose vertices lie on the circumference of a circle. One important property of cyclic quadrilaterals is that the sum of the opposite angles is equal to 180∘.
If A,B,C,D are the angles of the quadrilateral, then:
A+C=180∘andB+D=180∘
Hint: Recall the property of cyclic quadrilaterals regarding the sum of opposite angles.
2. Analyzing the Options:
We need to check the validity of the statements given in the options. Let's denote the options as follows:
- Option 1: tanA=−tanC
- Option 2: secB=−secD
- Option 3: sinB=sinD
- Option 4: (Assumed to be incorrect)
3. Checking Option 1:
From the property A+C=180∘:
tanA=tan(180∘−C)=−tanC
Thus, Option 1 is true.
Hint: Use the tangent subtraction identity for angles summing to 180∘.
4. Checking Option 2:
Again, using B+D=180∘:
secB=sec(180∘−D)=−secD
Thus, Option 2 is true.
Hint: Recall the secant function's behavior under angle transformations.
5. Checking Option 3:
Using B+D=180∘:
sinB=sin(180∘−D)=sinD
Thus, Option 3 is true.
Hint: Use the sine function's property for angles summing to 180∘.
6. Conclusion:
Since Options 1, 2, and 3 are all true, the only option left that is not true must be Option 4.
Final Answer:
The statement that is not true regarding the cyclic quadrilateral ABCD is Option 4.
A cyclic quadrilateral is a quadrilateral whose vertices lie on the circumference of a circle. One important property of cyclic quadrilaterals is that the sum of the opposite angles is equal to 180∘.
A+C=180∘andB+D=180∘
We need to check the validity of the statements given in the options. Let's denote the options as follows:
- Option 1: tanA=−tanC
- Option 2: secB=−secD
- Option 3: sinB=sinD
- Option 4: (Assumed to be incorrect)
From the property A+C=180∘:
tanA=tan(180∘−C)=−tanC
Thus, Option 1 is true.
Again, using B+D=180∘:
secB=sec(180∘−D)=−secD
Thus, Option 2 is true.
Using B+D=180∘:
sinB=sin(180∘−D)=sinD
Thus, Option 3 is true.
Since Options 1, 2, and 3 are all true, the only option left that is not true must be Option 4.
The statement that is not true regarding the cyclic quadrilateral ABCD is Option 4.
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS Book:CENGAGE ENGLISHChapter:TRIGONOMETRIC FUNCTIONS Exercise:Archives JEE Advanced Multiple correct answers type
Explore 1 Video
- TRIGONOMETRIC EQUATIONSBook:CENGAGE ENGLISHChapter:TRIGONOMETRIC EQUATIONSExercise:Archives (Matrix Match Type)
Explore 1 Video
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBook:CENGAGE ENGLISHChapter:TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASExercise:Matrix Match Type
Explore 1 Video
Similar Questions
Knowledge Check
If x+y=90∘, which of the following must be true?
Acosx=cosyBsin x=-sin yCtan x=cot yDsin x+cos y=1In the figure, ABCD is a rectangle. The area of quadrilateral EBFD is one half the area of the rectangle ABCD. Which one of the following is the value of AD ?
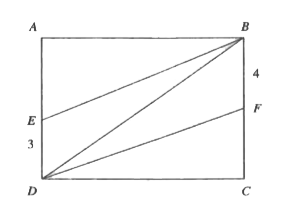 A5B6C7D12
A5B6C7D12Quadrilateral ABCD is a kite. Which of the followibng cannot be determined ?
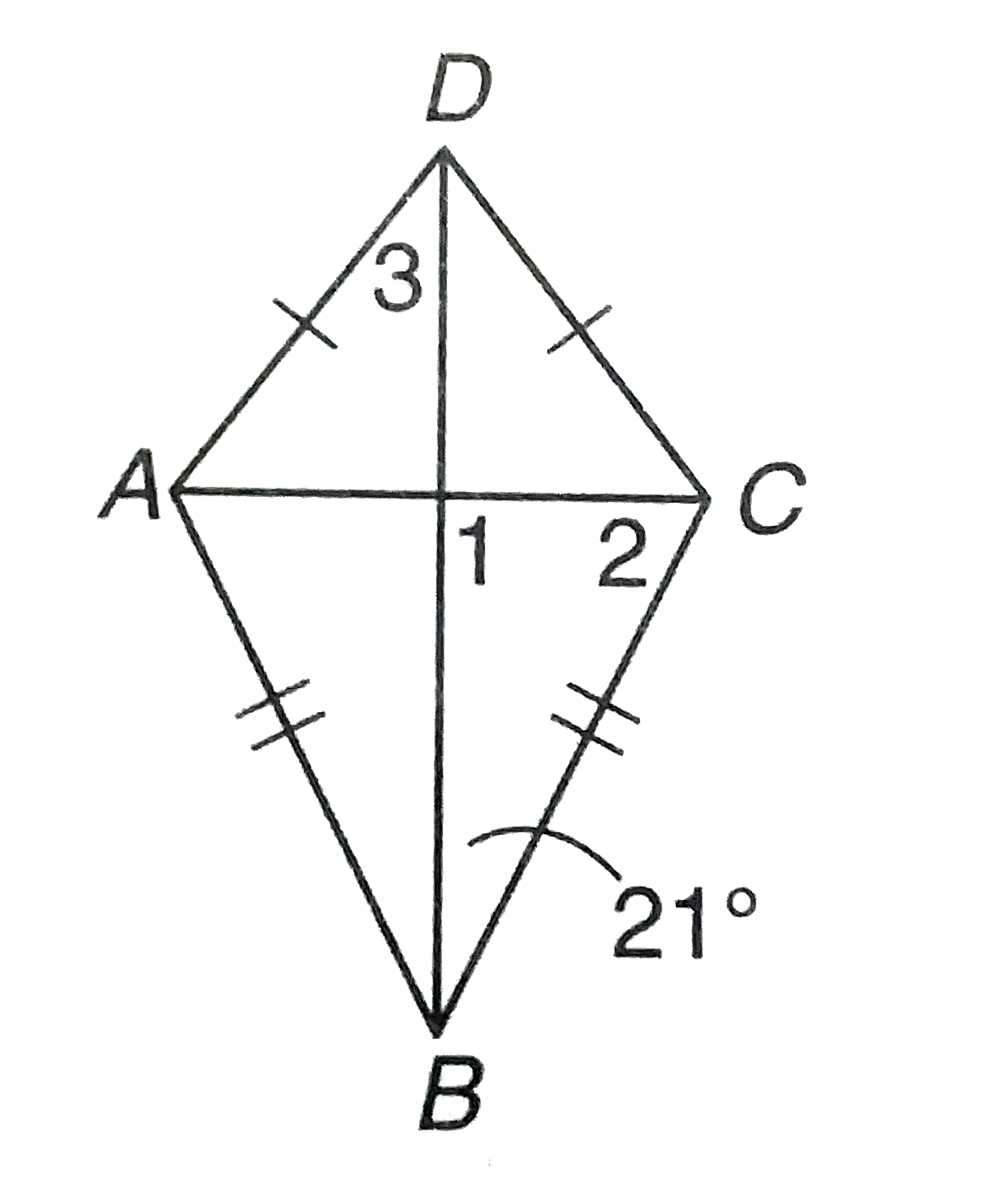 Am∠3=21∘Bm∠1=90∘Cm∠2=69∘DAD=CD
Am∠3=21∘Bm∠1=90∘Cm∠2=69∘DAD=CD
In a quadrilateral ABCD, −−→AB+−−→DC=
View SolutionIn a cyclic quadrilateral ABCD, the value of 2+∑cosAcosB, is
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 2s=a+b++c+d,a,b,candd are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
When the perimeter is minimum, the quadrilateral is necessarily
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 2s=a+b++c+d,a,b,candd are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
The minium perimeter of the quadrilateral is
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 2s=a+b++c+d,a,b,candd are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
The minimum value of the sum of the lenghts of diagonals is
View Solution

