Which of the following is not correct ?
cos(cos1)>cos(sin1)
sin(cos1)<sin(sin1)
cos(cos2)>sin(cos2)
none of these
The correct Answer is:D
To solve the problem of determining which of the following options is not correct, we will analyze each option step by step.
Step 1: Understand the Trigonometric Values
We know that:
- For angles less than π4 (or 45 degrees), cos(x)>sin(x).
- For angles greater than π4, sin(x)>cos(x).
- The values of sin(x) and cos(x) range between 0 and 1.
Step 2: Analyze Each Option
Let's denote the options as follows:
1. cos(cos(1))>sin(sin(1))
2. sin(cos(1))<sin(sin(1))
3. cos(cos(2))>sin(cos(2))
4. None of these
Option 1: cos(cos(1))>sin(sin(1))
- Since 1 radian is greater than π4, we know cos(1)<sin(1).
- Therefore, cos(cos(1))<cos(1) and sin(sin(1))>sin(1).
- Thus, cos(cos(1))<sin(sin(1)) is likely true.
Option 2: sin(cos(1))<sin(sin(1))
- Since cos(1)<π4, we have sin(cos(1))>sin(sin(1)).
- Therefore, this option is incorrect.
Option 3: cos(cos(2))>sin(cos(2))
- Since 2 radians is also greater than π4, we have cos(2)<sin(2).
- Thus, cos(cos(2))<sin(cos(2)), making this option also incorrect.
Step 3: Conclusion
From our analysis:
- Option 1 is correct.
- Option 2 is incorrect.
- Option 3 is also incorrect.
Thus, the answer to the question "Which of the following is not correct?" is Option 2.
We know that:
- For angles less than π4 (or 45 degrees), cos(x)>sin(x).
- For angles greater than π4, sin(x)>cos(x).
- The values of sin(x) and cos(x) range between 0 and 1.
Let's denote the options as follows:
1. cos(cos(1))>sin(sin(1))
2. sin(cos(1))<sin(sin(1))
3. cos(cos(2))>sin(cos(2))
4. None of these
- Since 1 radian is greater than π4, we know cos(1)<sin(1).
- Therefore, cos(cos(1))<cos(1) and sin(sin(1))>sin(1).
- Thus, cos(cos(1))<sin(sin(1)) is likely true.
- Since cos(1)<π4, we have sin(cos(1))>sin(sin(1)).
- Therefore, this option is incorrect.
- Since 2 radians is also greater than π4, we have cos(2)<sin(2).
- Thus, cos(cos(2))<sin(cos(2)), making this option also incorrect.
From our analysis:
- Option 1 is correct.
- Option 2 is incorrect.
- Option 3 is also incorrect.
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS Book:CENGAGE ENGLISHChapter:TRIGONOMETRIC FUNCTIONS Exercise:Archives JEE Advanced Multiple correct answers type
Explore 1 Video
- TRIGONOMETRIC EQUATIONSBook:CENGAGE ENGLISHChapter:TRIGONOMETRIC EQUATIONSExercise:Archives (Matrix Match Type)
Explore 1 Video
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBook:CENGAGE ENGLISHChapter:TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASExercise:Matrix Match Type
Explore 1 Video
Similar Questions
Knowledge Check
Which of the following is the correct match ?
ALamprey - ChondrichthyesBSaw fish - CyclostomataCSea horse - OsteichthyesDHagfish - OsteichthyesWhich of the following is the correct match ?
AAmyloplasts - Store carbohhydratesBElaioplasts - Store fast and oilsCAleuroplasts - Store proteinsDAll of these
Which of the following is a correct statement?
View SolutionWhich of the following is/are correct?
View SolutionWhich of the following is/are correct?
View SolutionWhich of the following is/are correct?
View SolutionWhich of the following match is correct ?
View Solution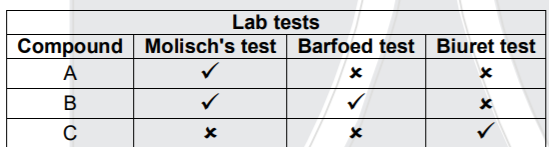 Which of the following options is correct ?
Which of the following options is correct ?
View Solution