Rectangle ABCD has area 200.An ellipse with area passes through A and C and has foci at B and D. Find the perimeter of the rectangle.
Let the sides of reactangle be p and q.
Area or reactangle

Area of ellipse
Perimeter of rectangle =2(p+q)
From triangle ABD,
Distance = Distance between foci
Also, from the definition of ellipse, the sum of focal lengths is 2a. Then,
Putting the value of (p+q) in (3) from (4), we have
[Using (1)]
From (2),
Since [ From (4)]
Perimete
Similar Questions
Knowledge Check
AC, a diagnonal of the rectange ABCD , measure 5 units. The area of the rectangle is 12 sq. units. What is the perimeter of the rectangle?
A7B14C17D20In the figure, ABCD is a rectangle, and F and E are points on AB and BC respectively. The area of ΔDFB is 9 and the area of ΔBED is 24. What is the perimeter of the rectangle?
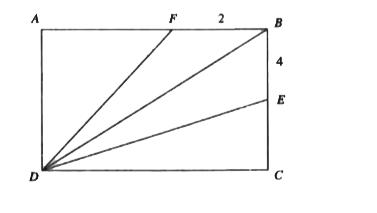 A18B23C30D42
A18B23C30D42
The area of a rectangle is 49cm2 and its breadth is 2.8cm. Find the length of the rectangle.
View SolutionIf a rectangle has breadth 11 m and area 264 sq. m, what is the length of the rectangle? Also, find the perimeter of the rectangle.
View SolutionParallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View SolutionThe area of a square and a rectangle are equal.If the side of the square is 40 cm and the breadth of the rectangle is 25 cm,find the length of the rectangle. Also,find the perimeter of the rectangle.
View SolutionA square and a rectangle have equal area. If side of a square is 24 cm and the length of the rectangle is 32 cm , find
the breadth of the rectangle
View SolutionIn rectangle ABCD, diagonal BD = 26 cm and cotangent of angle ABD = 1.5. Find the area and the perimeter of the rectangle ABCD.
View Solution