The point of intersection of the tangents at the point P on the ellipse x2a2+y2b2=1 and its corresponding point Q on the auxiliary circle meet on the line x=ae (b) x=0 y=0 (d) none of these
x=a/e
x=0
y=0
none of these
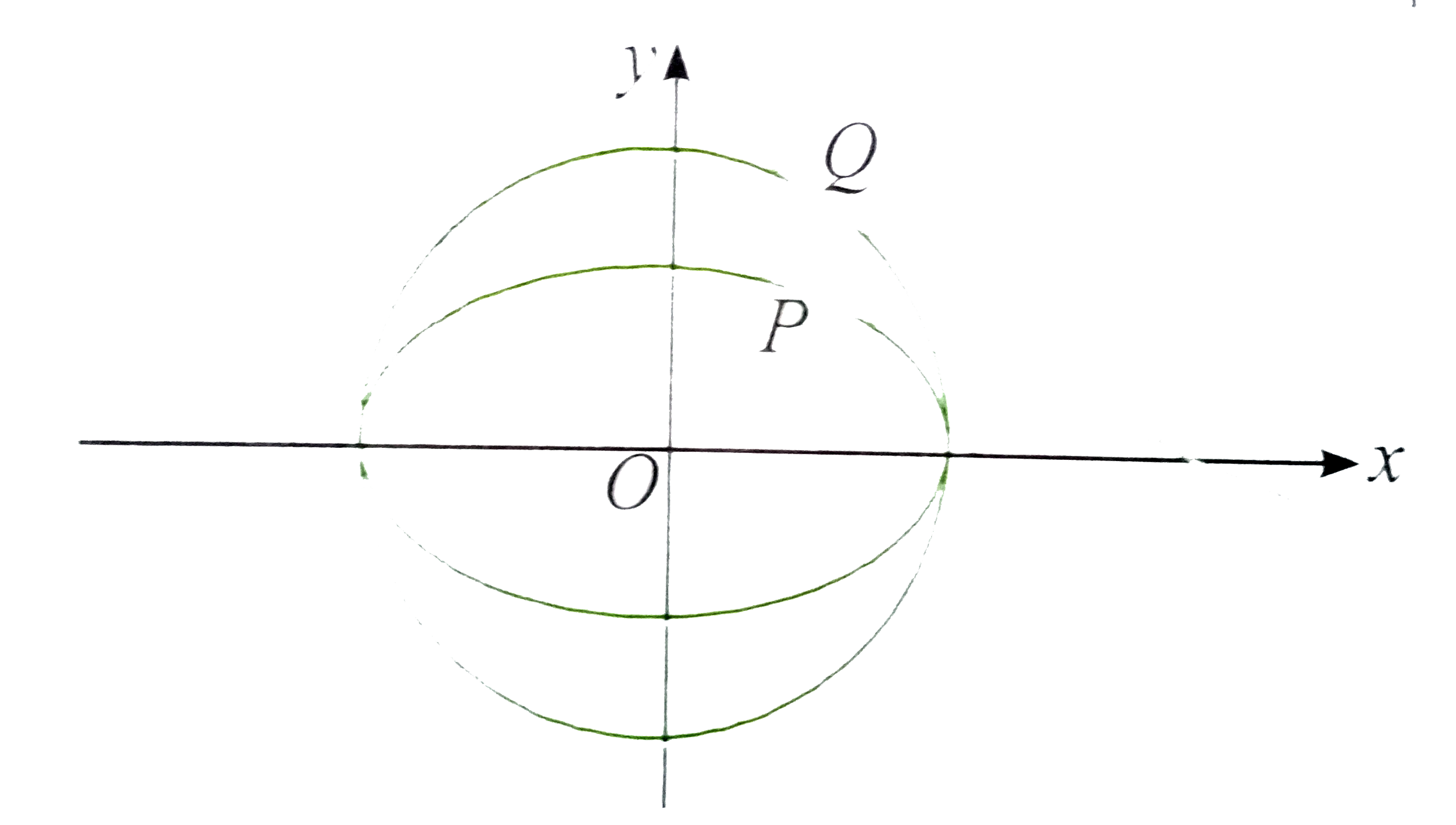
Tangent to the ellipse at point P(acosθ,asinθ) is xacosthea+ybsinθ=1(1)
Tangent (1) and (2) intersect at (a/cosθ,0) which lies on y=0
Similar Questions
The point of intersection of the tangents at the point P on the ellipse x2a2+y2b2=1 and its corresponding point Q on the auxiliary circle meet on the line (a) x=ae (b) x=0 (c) y=0 (d) none of these
View SolutionThe locus of the point of intersection of tangents to the ellipse x2a2+y2b2=1 which meet at right , is
View SolutionThe point of intersection of tangents drawn to the hyperbola x2a2−y2b2=1 at the points where it is intersected by the line lx+my+n=0 is
View SolutionThe locus of the point of intersection of tangents to the ellipse x2a2+y2b2=1 at the points whose eccentric angles differ by π/2, is
View SolutionThe locus of the point of intersection of tangents to the ellipse x2a2+y2b2=1 at the points whose eccentric angles differ by π/2, is
View SolutionThe locus of point of intersection of tangents to an ellipse x2a2+y2b2=1 at two points the sum of whose eccentric angles is constant is
View SolutionThe locus of point of intersection of tangents to an ellipse x2a2+y2b2=1 at two points the sum of whose eccentric angles is constant is
View SolutionThe locus of the point of intersection of the tangent at the endpoints of the focal chord of the ellipse x2a2+y2b2=1(b<a)(a) is a an circle (b) ellipse (c) hyperbola (d) pair of straight lines
View SolutionThe line x=at2 meets the ellipse x2a2+y2b2=1 in the real points iff
View SolutionThe locus of the point of intersection of the perpendicular tangents to the circle x2+y2=a2,x2+y2=b is
View Solution