Question

Let $A(-4,0)$ and $B(4,0)$. Then the number of points $C=(x,y)$ on the circle $x^2+y^2=16$ lying in first quadrant such that the area of the triangle whose vertices are A,B and C is a integer is

Answer

62

Explanation

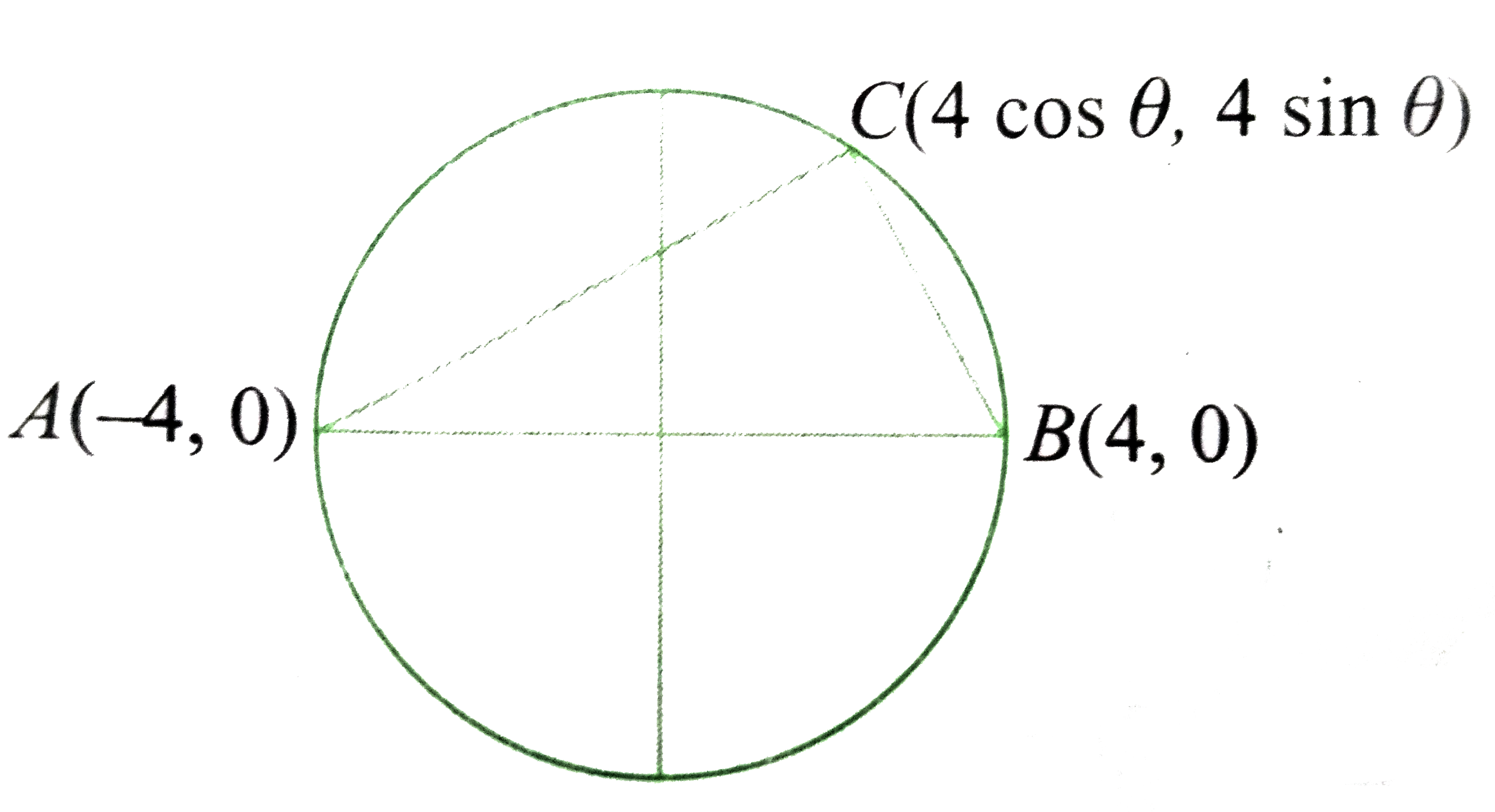
Required area
`A =(1)/(2)xx8xx|4 sin theta|= | 16 sin theta |`
Now, the area is an integer. Then the possible values of `sin theta` are
`(1)/(16),(2)/(16),.....,(15)/(16)`
i.e., 15 points in each quadrant or `60+2` more with `sin theta =1`.
Therefore,` N =62` lt