Question

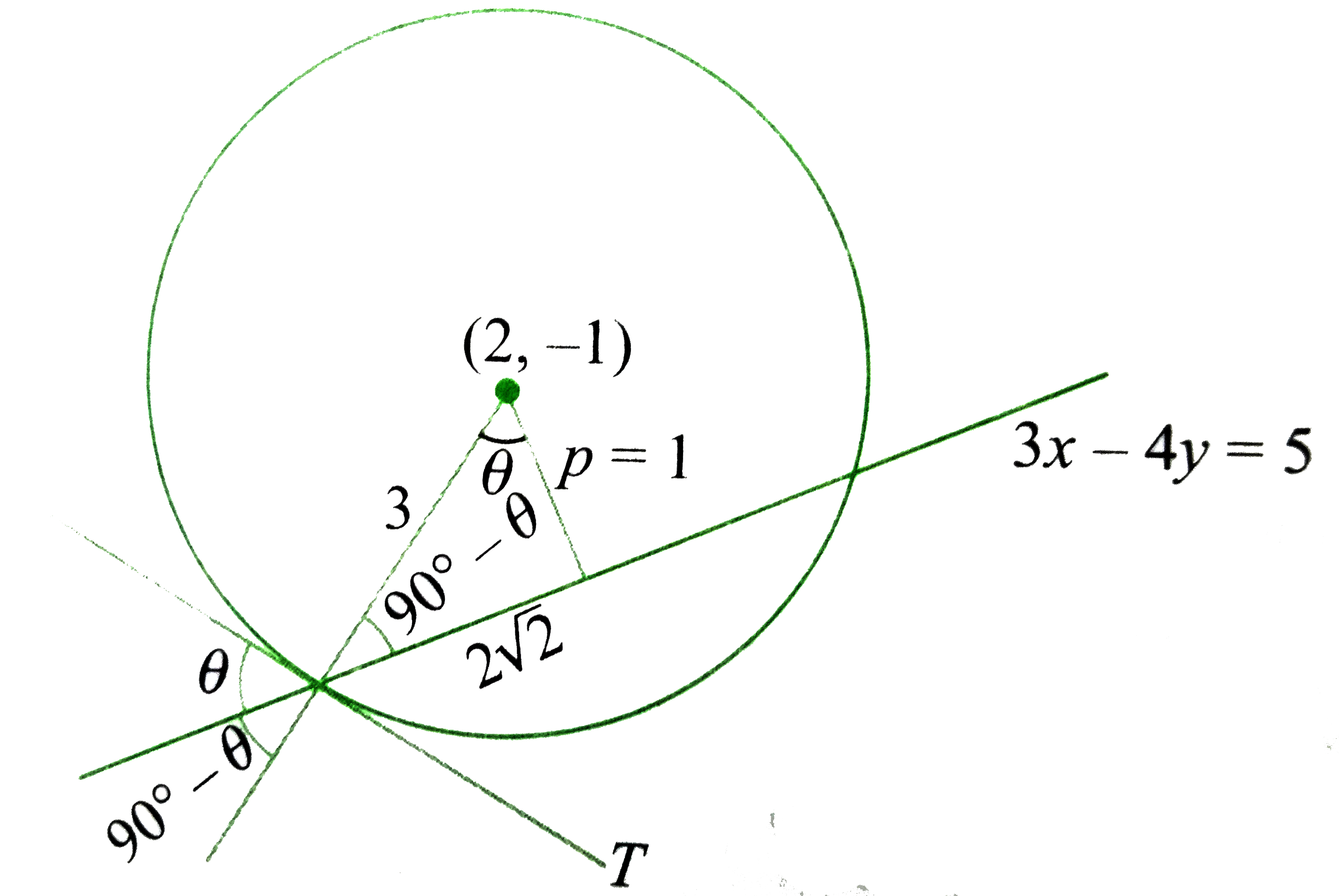
The acute angle between the line $3x-4y=5$
and the circle $x^2+y^2-4x+2y-4=0$
is $\theta$
. Then $9\cos \theta =$

Answer

3

Explanation

`theta` is the angle between the tangent and the line
The circle has center `(2,-1)` and radius 3.
The length of perpendicular from the center on `3x-4y=5` is
`p= | (6+4-5)/(5)|=1`
or `sin (90-theta)=(1)/(3)`
or `cos theta =(1)/(3)`