Let P and Q are points on the parabola $y^{2} = 4 a x$ with vertex O, such that OP is perpendicular to OQ and have lengths $r_{1} and r_{2}$ respectively, then the value of $\frac{r_{1}^{4 / 3} r_{2}^{4 / 3}}{r_{1}^{2 / 3} + r_{2}^{2 / 3}}$ is :

A

$16 a^{2}$

B

$a^{2}$

C

$4 a$

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

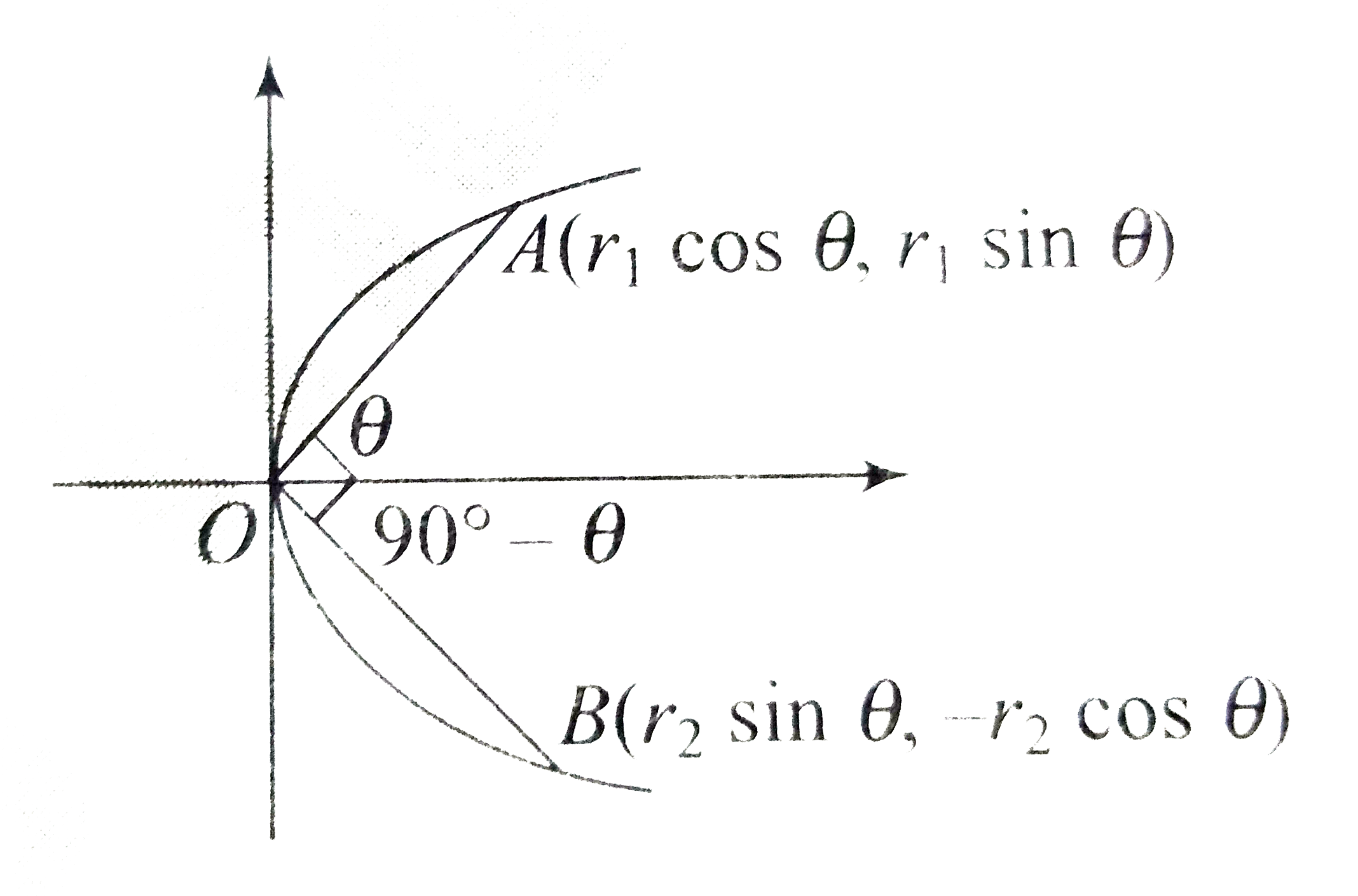
$r_{1}^{2} {sin}^{2} θ = 4 a r_{1} cos θ$ (i)
and $r_{2}^{2} {cos}^{2} θ = 4 a r_{2} sin θ$ (ii)
From Eq. (i), we get $r_{1}^{2} {sin}^{4} θ = 16 a^{2} {cos}^{2} θ$ (iii)
from Eqs. (ii) and (iii), we get
${sin}^{3} θ = \frac{64 a^{3}}{r_{1}^{2} r_{2}}$ (iv)
similarly, ${cos}^{3} θ = \frac{64 a^{3}}{r_{1} r_{2}^{2}}$
Eliminating $θ$ , we get
$\frac{r_{1}^{4 / 3} r_{2}^{4 / 3}}{r_{1}^{2 / 3} + r_{2}^{2 / 3}} = 16 a^{2}$

|

Updated on:21/07/2023

Class 12 MATHS PARABOLA

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-PARABOLA-Single Correct Answer Type

Home
Ask Doubt
Profile