Question

Tangents $PA$
and $PB$
are drawn to $x^2+y^2=9$
from any arbitrary point $P$
on the line $x+y=25$
. The locus of the midpoint of chord $AB$
is
$25(x^2+y^2)=9(x+y)$

$25(x^2+y^2)=3(x+y)$

$5(x^2+y^2)=3(x+y)$

$noneofthese$

Options

A. `x^(2)+y^(2) -2x -2y = 0`
B. `x^(2) +y^(2) +2x +2y = 0`
C. `x^(2) +y^(2) - 2x +2y = 0`
D. `x^(2) +y^(2) +2x - 2y= 0`

Answer

A

Explanation

Let `P(a,4-a)`.

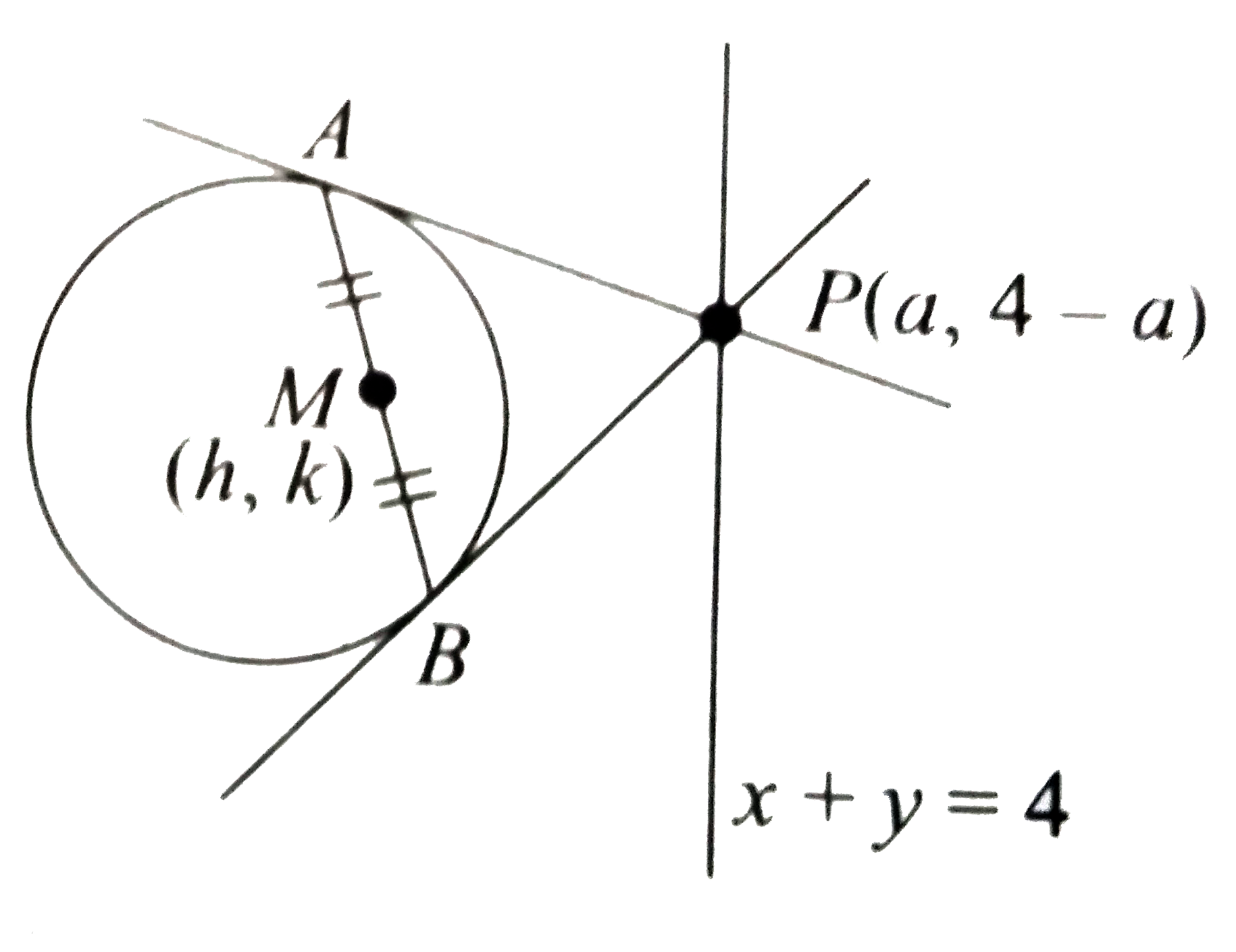
The equation of chord of contact AB is
`xa +y (4-a) =8` (i)
Also, equation of chord AB whose mid-points is `M(h,k)` is
`hx + ky = h^(2) +k^(2)` (ii) (using `T = S_(1))`
Since (i) and (ii) are identical, on comparing the coefficients, we get
`(a)/(h) =(4-a)/(k) = (8)/(h^(2) +k^(2)) =(a+4-a)/(h+k) =(4)/(h+k)`
`rArr 4(h^(2)+k^(2)) =8(h+k)`
Hence, locus of `M(h,k)` is `x^(2) +y^(2) -2x -2y =0`.