Draw the graph of y=loge(x+√x2+1)

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

We have y=f(x)=loge(√1−x2−x)
f(x) is defined if √1−x2−x>0 and 1−x2≥0
For 1−x2≥0,−1≤x≤1
√1−x2−x>0
For (0,1),
1−x2>x2
or 0<x<1√2
Thus, the domain of the function is [−1,1√2]
f′(x)=(−x√1−x2)−1√1−x2−x
=−x−√1−x2(√1−x2√1−x2−x)
f′(x)=0∴−x=√1−x2
∴x=−1√2
f′(x)>0 for x∈(−1,−1√2)
f′(x)<0 for x∈(−1√2,1√2)
So x=−1√2 is the point of maxima.
f(−1)=f(0)=0
limx→1√2loge(√1−x2−x)=−∞⎛⎜⎝∴limx→1√2(√1−x2−x)=0⎞⎟⎠
Thus, x=1√2 is an asymptote.
From the above discussion, the graph of the function is as shows in the following figure.
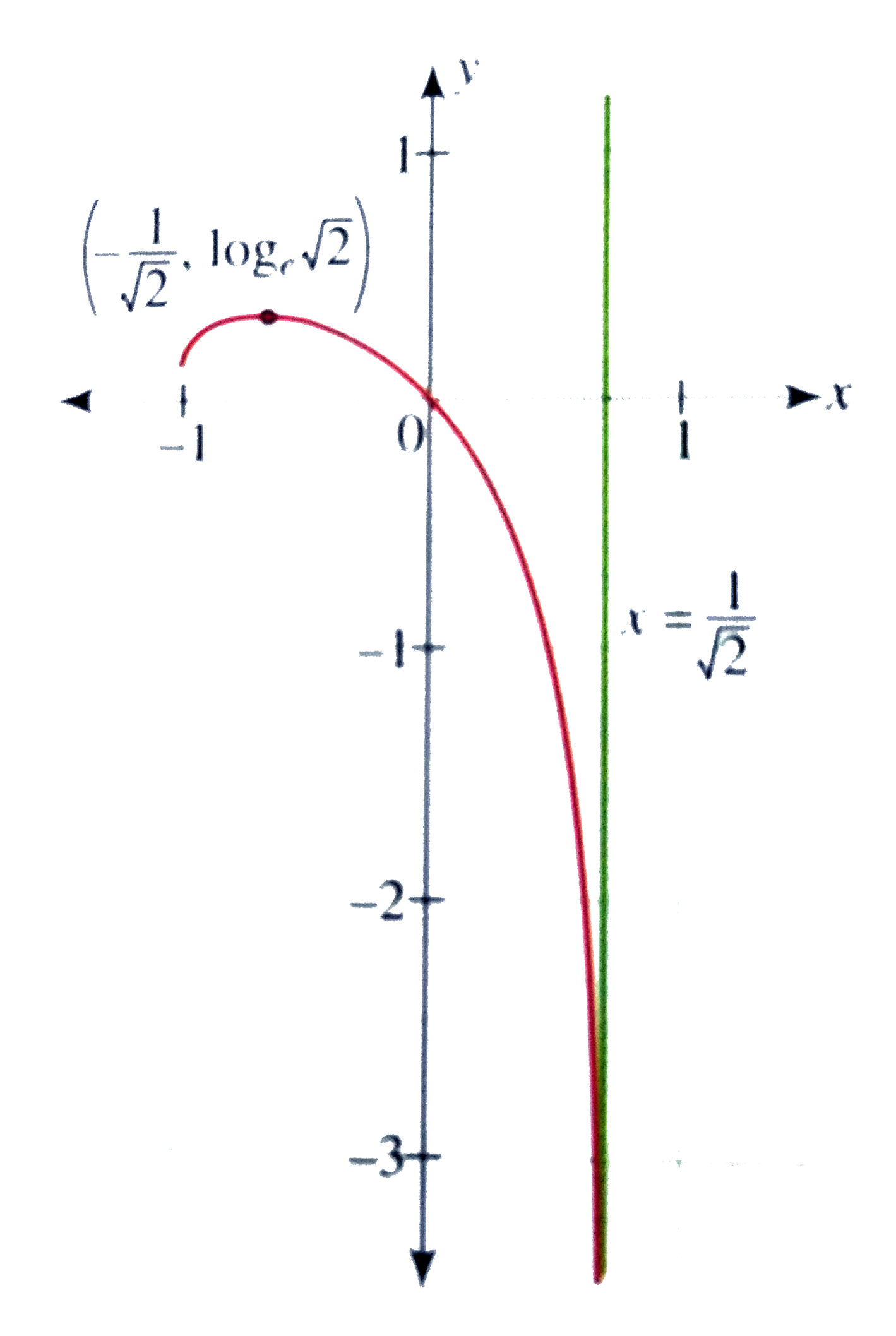
ocr_image

|