Question

Draw the graph of ${\displaystyle f\left(x\right)=\frac{e^x}{1+e^x}}$. Also find the point of inflection.

Explanation

`f(x) = e^(x)/(1+e^(x))`
`rArr r^(')(x) = (e^(x)(1+e^(x))-e^(x)e^(x))/((1+e^(x))^(2))=e^(x)/(1+e^(x))^(2) gt 0 AA x in R`
So `f(x)` is an increasing function.
Also, `lim_(x to infty) (e^(x)/(1+e^(x))) =0` and `lim_(x to infty) (e^(x)/(1+1/e^(x)))=1`
Hence the graph of `f(x)=e^(x)/(1+e^(x))` is as shown in the following figure.

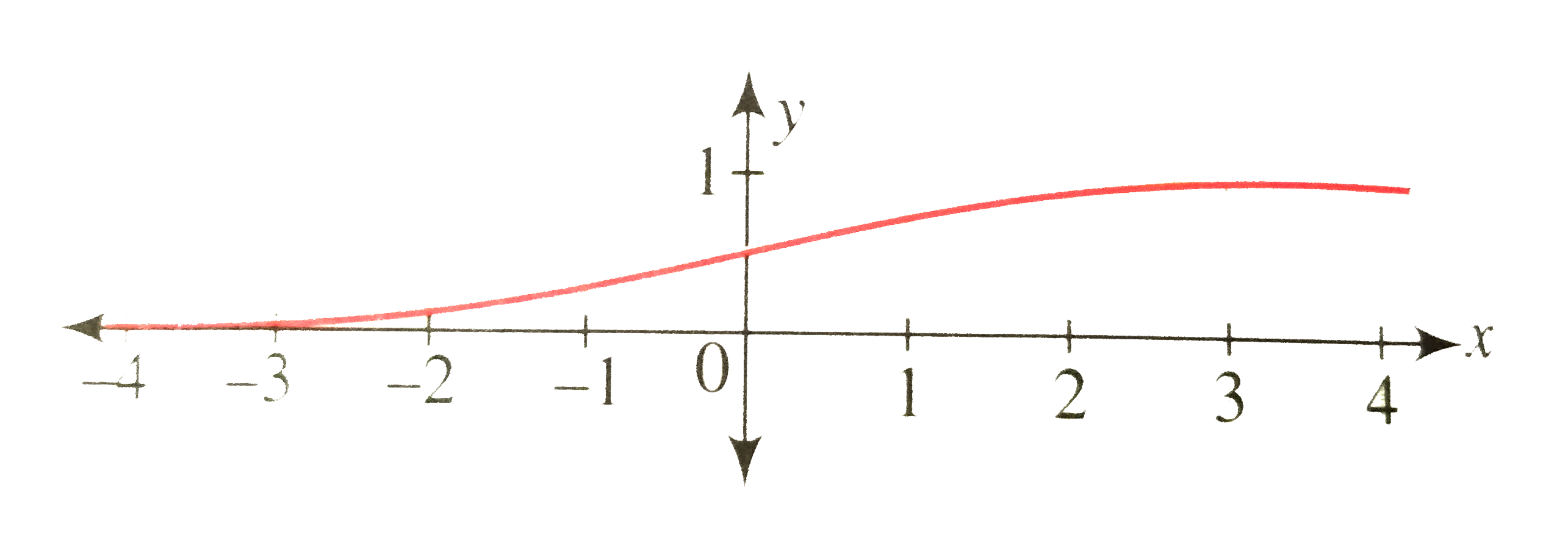
Clearly, from the graph, y=0 and y=1 are asymptotes.
Also `f^('')(x)=(e^(x)(1+e^(x))^(2)-2(1+e^(x))e^(x)e^(x))/(1+e^(x))^(4)=0`
`rArr (1+e^(x))-2e^(x)=0`
`rArr e^(x)=1`
So `x=0` is the point of inflection where the curve its concavity as shown in the figure.