Draw the graph of y=xex. Find the range of the function. Also find the point of inflection.
We have y=f(x)=xex
Clearly, the domain of the function is R.
f(0)=−0
and f(x)=0 when x=0
f′(x)=ex+xex=ex(1+x)
f′(x)>0 for x<−1, where f(x) increases
f′(x)<0 for x<−1, where f(x) decreases
f′(x)=0∴x=−1
Also at x=−1,dydx, Changes sign from negative to positive, hence x=−1 is the point of minima,
f(−1)=−e−1=−1/e
When x→∞,f(x)→∞
Also limx→−∞xex=xx→−∞e−x=1x→−∞−e−x=0
So x-axis is an asymptote.
Thus, in (−∞,−1),f(x) decreases from 0+→−1/e
In (1,∞),f(x) increases, intersecting the x-axis at x=0
f''(x)=ex(2+x)
f''(x)=0∴x=−2
So x=−2 is the point of inflection.
From the above discussion, the graph of the function is as follows:
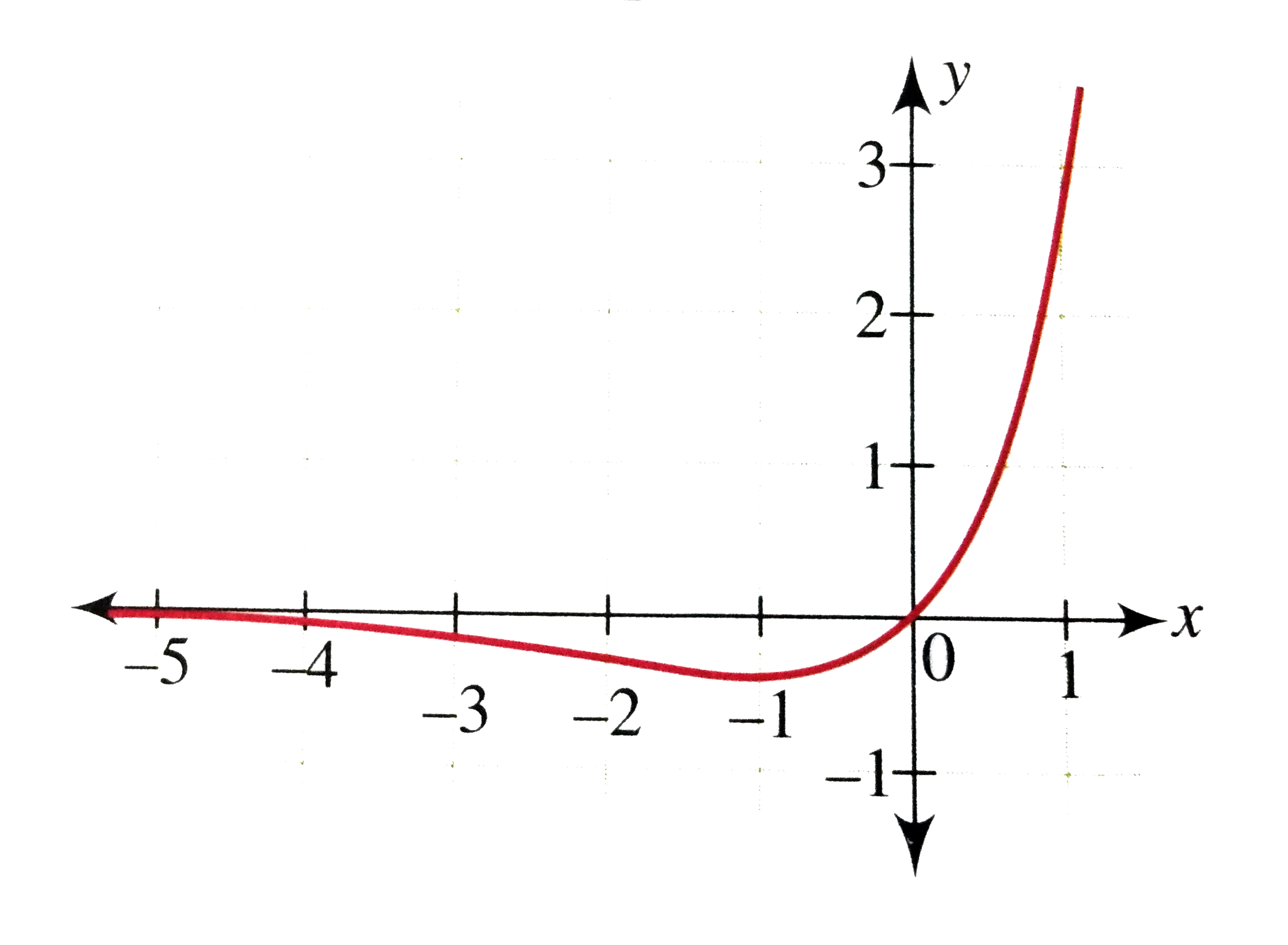
Range of the function is [f(−1),∞) or [−e−1,∞).
Topper's Solved these Questions
Similar Questions
Draw the graph of f(x)=|x|−|2x−3|. Find the range of the function.
View SolutionDraw the graph of f(x)=|2x−1|+|2x−3|. Find the range of the function.
View SolutionDraw the graph of f(x)=|x−1|+|2x−3|. Find the range of the function.
View SolutionDraw the graph of f(x)=loge(√1−x2).Find the range of the function .Also find the values of k if f(x) has two distinct real roots.
View SolutionFind the range of function y=ln(2x−x2)
View SolutionDraw the graph of f(x)=2x+3x2/3 and discuss the type of non-differentiability for the function. Also find the point of inflection.
View SolutionLet f(x)=[x]+1{x}+1 for f:[0,52)→(12,3], where [⋅] represents the greatest integer function and {⋅} represents the fractional part of x.
Draw the graph of y=f(x). Prove that y=f(x) is bijective. Also find the range of the function.
View SolutionDraw the graph of y = tan x and find the period.
View SolutionDraw the graph of y = cot x and find the period.
View SolutionFind the points of local maxima or local minima and corresponding local maximum and local minimum values of each of the given function. Also, find the points of inflection, if any : f(x)=xex
View Solution