Draw the graph of y=2cosx+sin2x
Video Solution
Text Solution
We have y=f(x)=2cosx+sin2x
Clearly, domain of the function is R.
Also f(x) is periodic with period 2π.
So we need to draw the graph for the interval for the interval [0,2π].
f(0)=0
f(x)=0
∴2cosx+2sincosx=0
∴2cosx(1+sinx)=0
∴cosx=0 or sinx=−1
∴x=π/2 or x=(3π)/2
f′(x)=−2sinx+2cosx2x
=−2(2sin2x+sinx−1)
=−2(2sinx−1)(sinx+1)
f′(x)=0
∴sinx=1/2 or sinx=−1
∴x=π/6,5π6 or x=3π2
f(π/6)=2cos(π/6)+sin(π/3)
=3√32
f(5π/6)=2cos(5π/6+sin(5π/3))
=−3√32
f(3π/2)=0
So important points on graph paper as shown in the following figure.
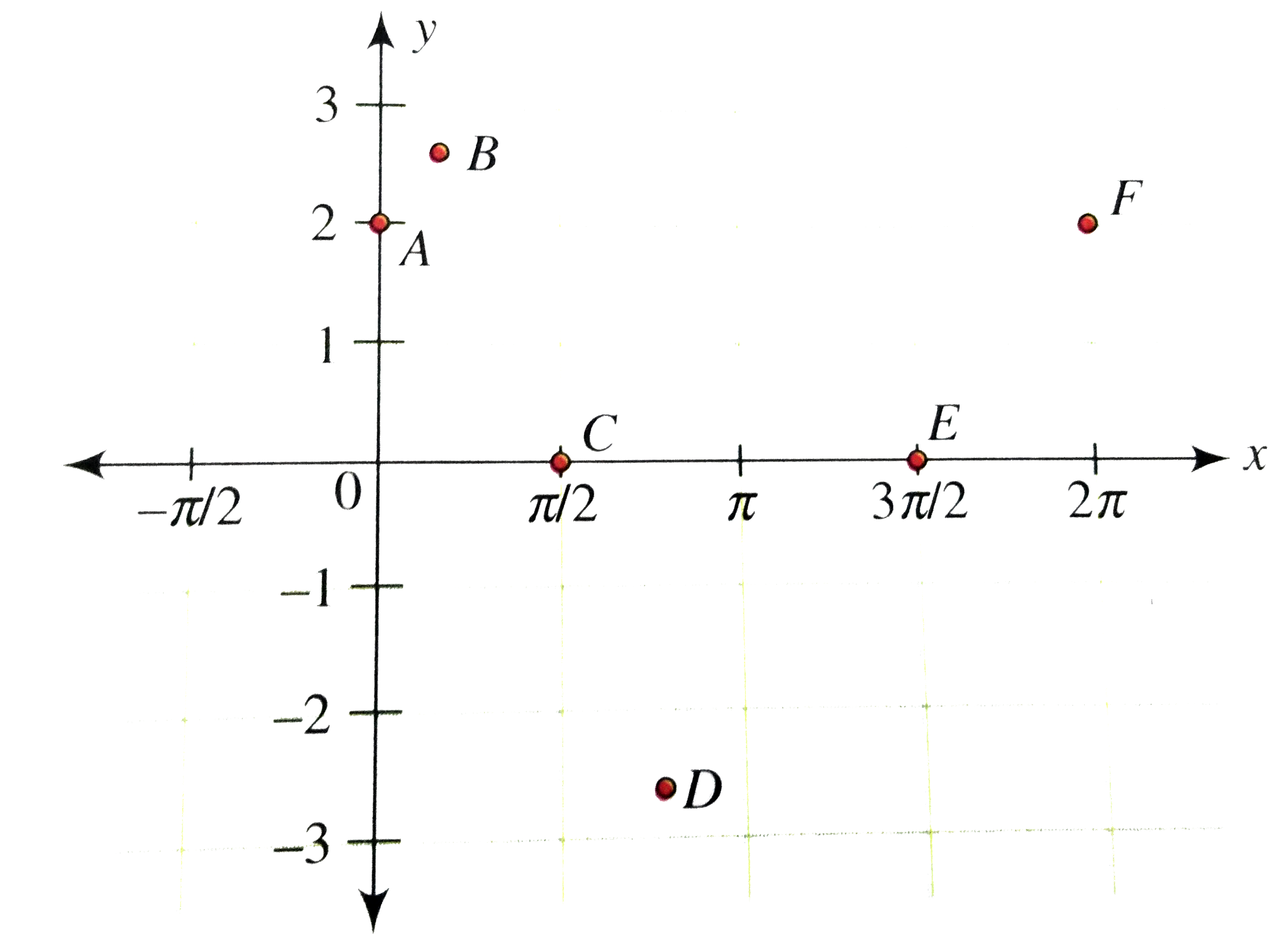
From the points A to B, f(x) increases, from points B to D, f(x) decreases intersecting the x-axis at C, from points D to F, f(x) increases intersecting the x-axis at E.
Further f''(x)=−2cosx−4sin2x
f''(x)=0 at x=(3π/2), hence it is the point of inflection.
Since functions have period 2π, the graph of y=f(x) for x∈R is as shown in the following figure.
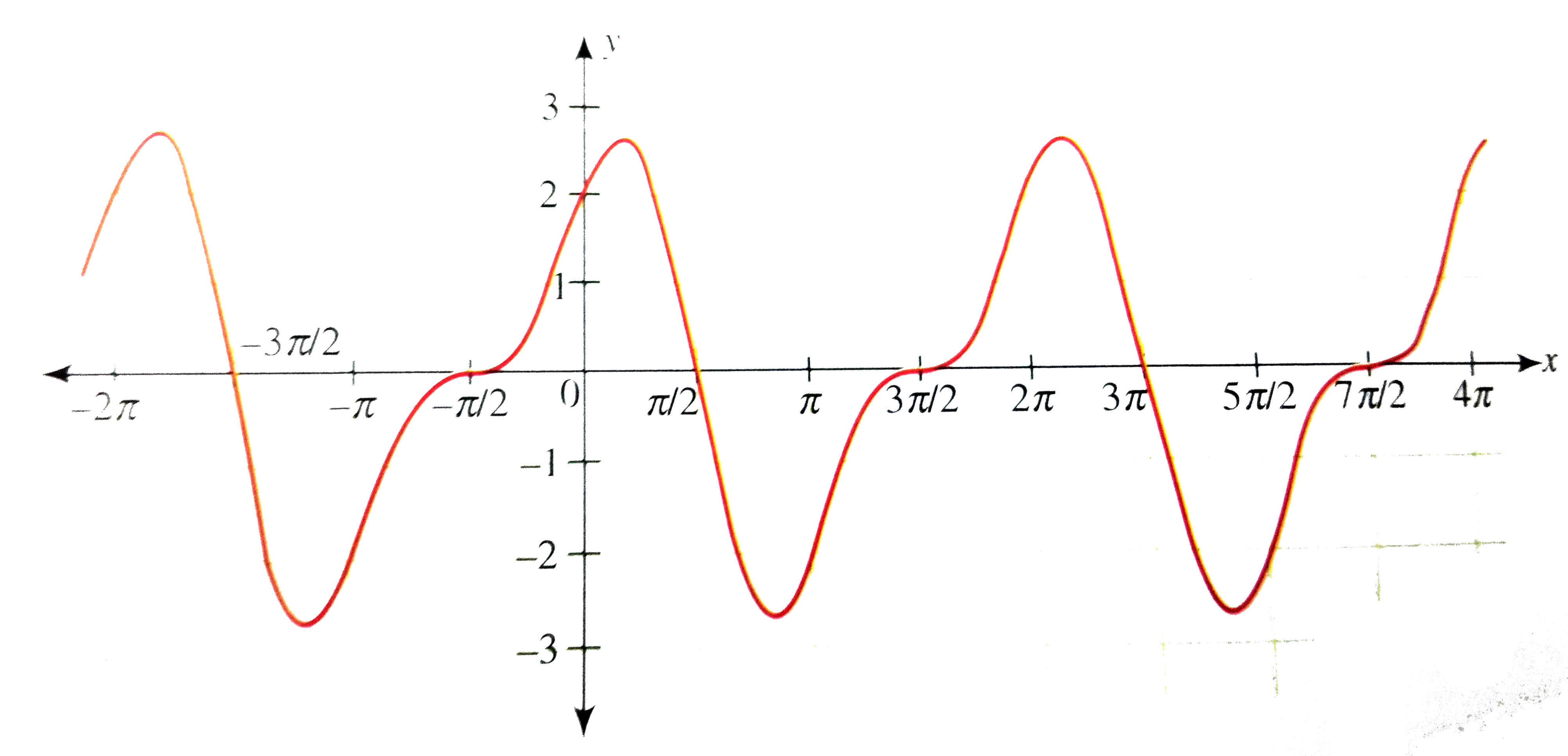
|
Topper's Solved these Questions
Similar Questions
Draw the graph of y=2x.
View SolutionDraw th graph of y=−2x
View SolutionDraw the graph of y=2x−1
View SolutionDraw the graph of y=2x.
View SolutionDraw the graph of y=|7−2x|
View SolutionDraw the graph of y=|x|+2
View SolutionDraw the graph of y=sin|x|.
View SolutionDraw the graph of y=2−x.
View SolutionDraw the graph of y=−2x+32
View SolutionDraw the graph of y=3sin2x
View Solution
