The area of the region $R = {\begin{matrix} x & y \end{matrix} | x | \leq | y ∣ and x^{2} + y^{2} \leq 1}$ is

A

$\frac{1}{2} < α < 1$

B

$α^{4} + 4 α^{2} - 1 = 0$

C

$0 < α \leq \frac{1}{2}$

D

$2 α^{4} - 4 α^{2} + 1 = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, D

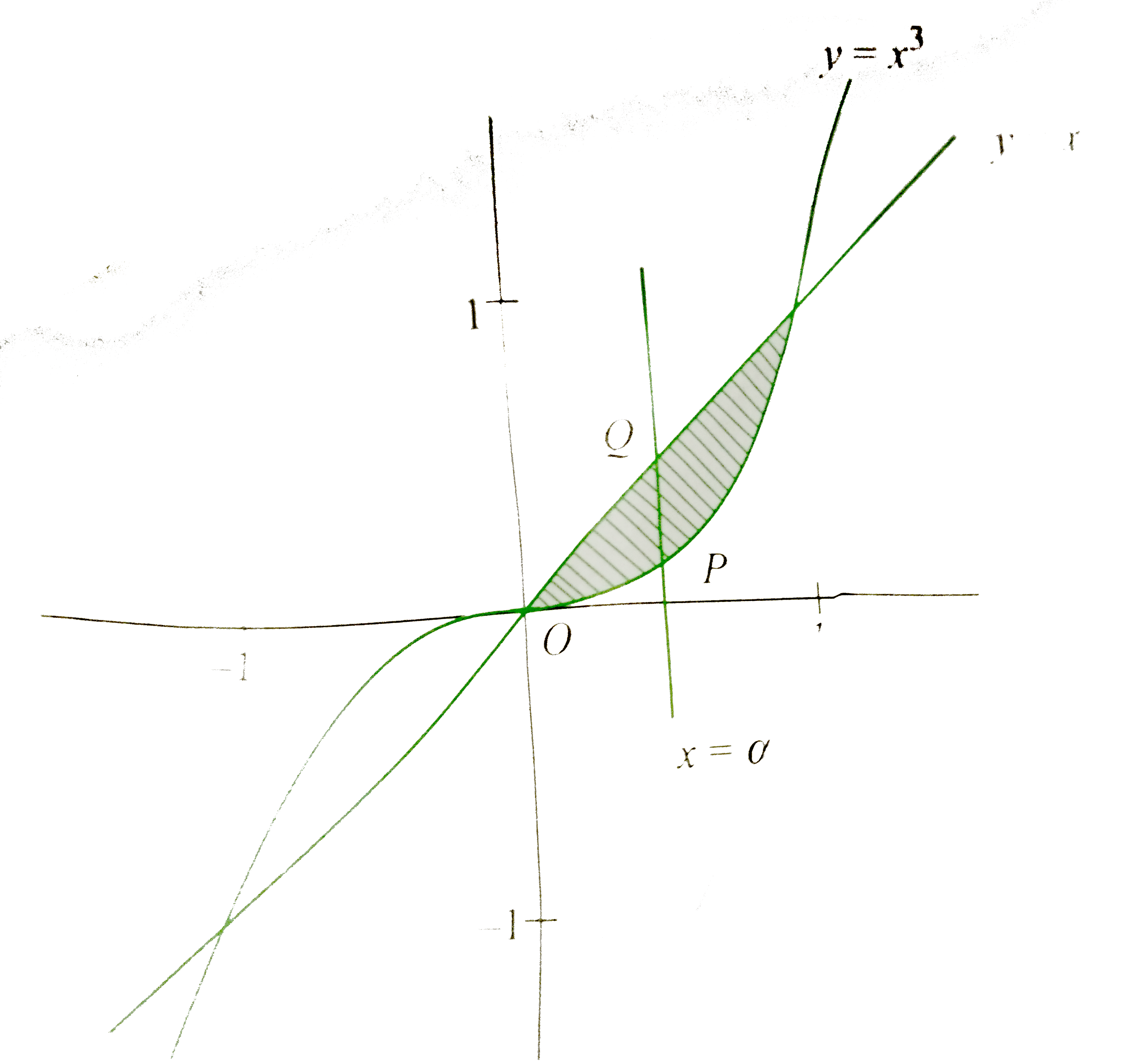
Area between $y = x^{3} and y = x in x \in (0, 1)$ is
$A = 1 \int 0 (x - x^{3}) d x = \frac{1}{4}$
Area of curvilinear triangle $O P Q = \frac{A}{2} = \frac{1}{8}$
$\Rightarrow α \int 0 (x - x^{3}) d x = \frac{1}{8}$
$\Rightarrow 2 α^{4} - 4 α^{2} + 1 = 0$
$\Rightarrow {(α^{2} - 1)}^{2} = \frac{1}{2}$
$\Rightarrow α^{2} = \frac{\sqrt{2} - 1}{\sqrt{2}}$

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-AREA-Multiple Correct Answers Type

Home
Ask Doubt
Profile