The parabolas y2=4xandx2=4y divide the square region bounded by the lines x=4,y=4 and the coordinate axes. If S1,S2,S3 are the areas of these parts numbered from top to bottom, respectively, then S1:S2≡1:1 (b) S2:S3≡1:2 S1:S3≡1:1 (d) S1:(S1+S2)=1:2
S1:S2≡1:1
S2:S3≡1:2
S1:S3≡1:1
S1:(S1+S2)=1:2
The correct Answer is:A, C, D
y2=4xandx2=4y meet at O(0,0)andA(4,4).
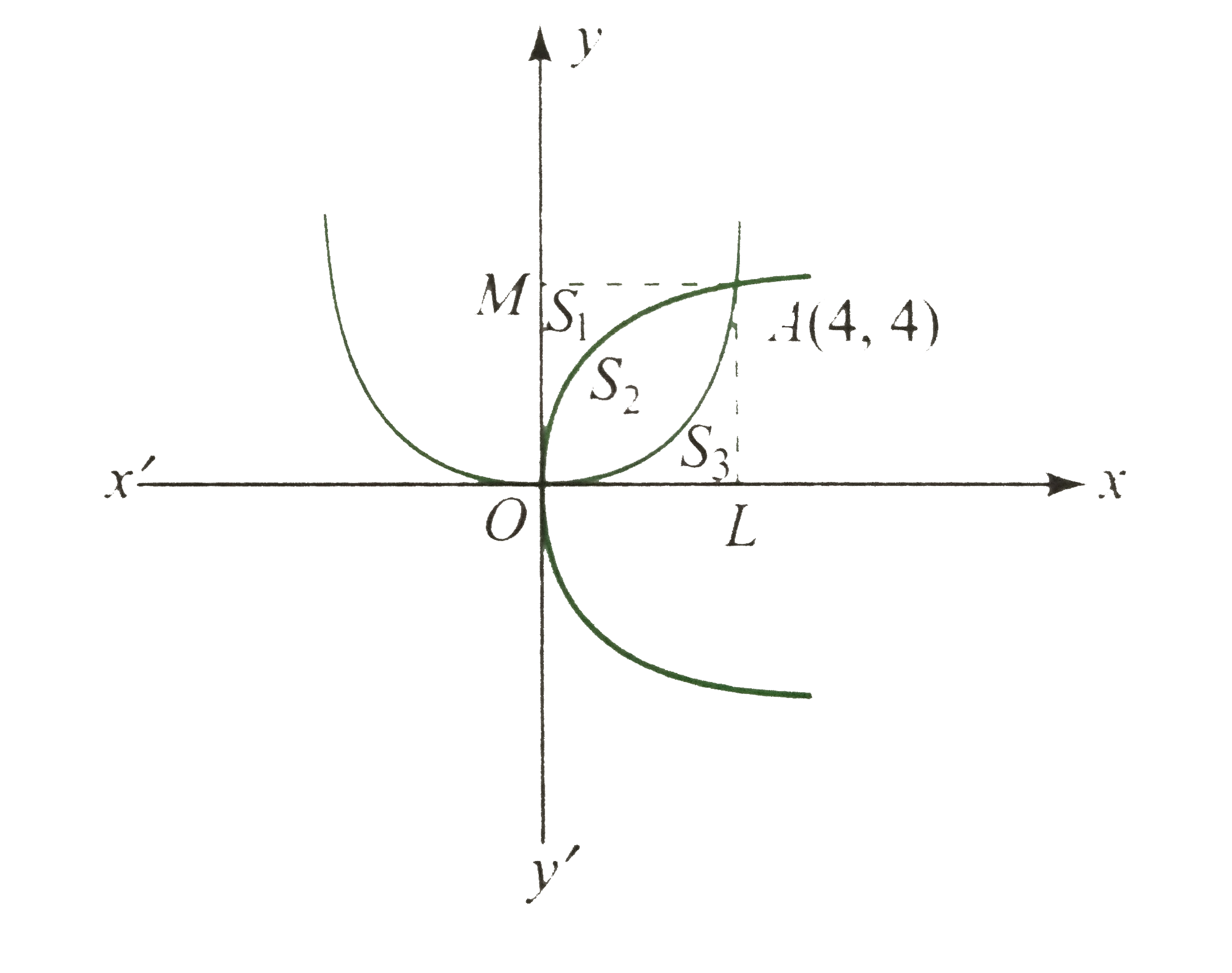
Now, S3=∫40x24dx=14[x33]40=112[64−0]=163.
S2=∫402√xdx−S3=2[x3/23/2]−163
=43[8−0]−163=163.
And S1=4×4−(S2+S3)=16−(163+163)=163.
Hence, S1:S2:S3=1:1:1
Topper's Solved these Questions
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Linkded Comprehension Type
21 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Matrix Match Type
5 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Exercises - Single Correct Answer Type
40 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
Similar Questions
If S1,S2,S3are the sum of first n natural numbers, their squares and their cubes, respectively, show that 9S22=S3(1+8S1).
View SolutionIf S1,S2,S3 are the sums of first n natural numbers, their squares and cubes respectively, show that 9S22=S3(1+8S1).
View SolutionIf S1,S2andS3 are the sums of first n natureal numbers, their squares and their cubes respectively, then S41S22−S22S23S21+S22=
View SolutionLet the sum of n, 2n, 3n terms of an A.P. be S1,S2and S3, respectively, show that S3=3(S2−S1).
View SolutionIf S1,S2 and S3 denote the sum of first n1,n2 and n3 terms respectively of an A.P. Then S1n1(n2−n3)+S2n2(n3−n1)+S3n3(n1−n2) equals :
View SolutionIf S1,S2,S3 be respectively the sums of n,2n,3n terms of a G.P., then prove that (S1)2+(S2)2=S1(S2+S3) .
View SolutionIf S1,S2andS3 be respectively the sum of n, 2n and 3n terms of a G.P., prove that S1(S3−S2)=(S2−S1)2
View SolutionIf S1 be the sum of (2n+1) term of an A.P. and S2 be the sum of its odd terms then prove that S1:S2=(2n+1):(n+1).
View SolutionThe sum of n, 2n, 3n terms of an A.P. are S1,S2,S3 respectively. Prove that S3=3(S2−S1)
View SolutionIf the sum of n,2n,3n terms of an AP are S1,S2,S3 respectively . Prove that S3=3(S2−S1)
View Solution
