The area of the closed figure bounded by y=x22−2x+2 and the tangents to it at (1,12)and(4,2) is 98sq.units (b) 38sq.units 32sq.units (d) 94sq.units
9/8 sq. units
3/8 sq. units
3/2 sq. units
9/4 sq. units
The correct Answer is:A
y=x22−2x+2=(x−2)22,
dydx=x−2,(dydx)x=1=−1,(dydx)x=4=2
Thus, tangent at (1,1/2) is y−1/2=−1(x−1)or2x+2y−3=0
Tangent at (4,2) is y−2=2(x−4)or2x−y−6=0
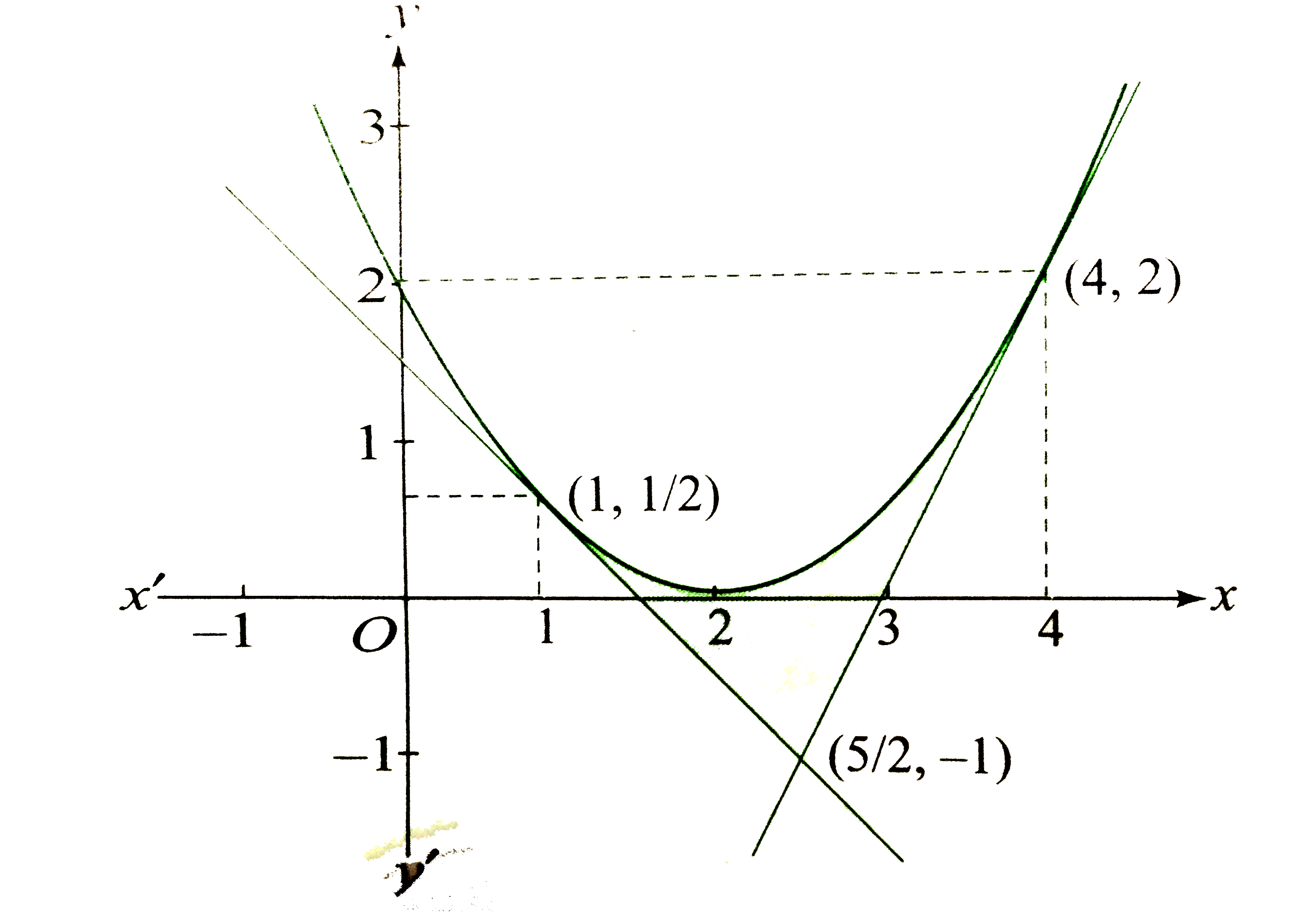
Hence, A=5/2∫1(x22−2x+2−3−2x2)dx+4∫5/2(x22−2x+2−(2x−6))dx
=4∫1(x22−2x+2)dx−5/2∫1(3−2x2)dx−4∫5/2(2x−6)dx
=(x36−x2+2x)41−12(3x−x2)5/21−(x2−6x)45/2
=(633−15+6)−12(3×32−(254−1))−((16−254)−6(4−52))
=32−12(92−214)−(394−6(32))
=98 sq. units
Topper's Solved these Questions
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Multiple Correct Answers Type
13 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Linkded Comprehension Type
21 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Concept Application Exercise 9.3
7 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
Similar Questions
The area of the closed figure bounded by x=−1,x=2,and y={−x2+2,x≤12x−1,x>1and the ascissa axis is (a)163sq.units (b) 103sq.units (c)133sq.units (d) 73sq.units
View SolutionLet f(x)=x3+3x+2andg(x) be the inverse of it. Then the area bounded by g(x) , the x-axis, and the ordinate at x=−2andx=6 is (a) 94sq.units (b) 43sq.units (c) 54sq.units (d) 73sq.units
View SolutionThe area bounded by the two branches of curve (y−x)2=x3 and the straight line x=1 is (a) 15sq.units (b) 35sq.units 45sq.units (d) 84sq.units
View SolutionThe area bounded by the two branches of curve (y−x)2=x3 and the straight line x=1 is 15sq.units (b) 35sq.units 45sq.units (d) 84sq.units
View SolutionThe area bounded by the curve a2y=x2(x+a) and the x-axis is a23sq.units (b) a24sq.units 3a24sq.units (d) a212sq.units
View SolutionA copper rod of mass m rests on two horizontal rails distance L apart and carries a current of I from one rail to the other. The coefficient of static friction between rod and rails is μs What are the (a) magnitude and (b) angle (relative to the vertical) of the smallest magnetic field that puts the rod on the verge of sliding?
View SolutionThe area of the region bounded by x=0,y=0,x=2,y=2,y≤ex and y≥1nx is (a) 6−41n2sq.units (b) 41n2−2sq.units 21n2−4sq.units (d) 6−21n2sq.units
View SolutionArea of the triangle formed by the line x+y=3 and the angle bisectors of the pairs of straight lines x2−y2+2y=1 is 2sq.units (b) 4sq.units 6sq.units (d) 8sq.units
View SolutionThe area bounded by the curve y2=8x and x2=8y is 163sq.units b. 316sq.units c. 143sq.units d. 314sq.units
View SolutionThe area of the smaller region bounded by circle x2+y2=1 and |y|=x+1 (a)π2−12sq.units (b) π2−1sq.units (c) π2sq.units (d) π2+1sq.units
View Solution
