Question

Find the area enclosed between the curves: $y={\log }_e(x+e),x={\log }_e\left(\frac{1}{y}\right)$ & the x-axis.

Options

A. 2 sq. units
B. 1 sq. units
C. 4 sq. units
D. None of these

Answer

A

Explanation

`y=log_(e)(x+e),x=log_(e)((1)/(y))or y=e^(-x).`
For `y=log_(e)(x+e),` Shift the graph of `y=log_(e)x,e` units to the left hand side.

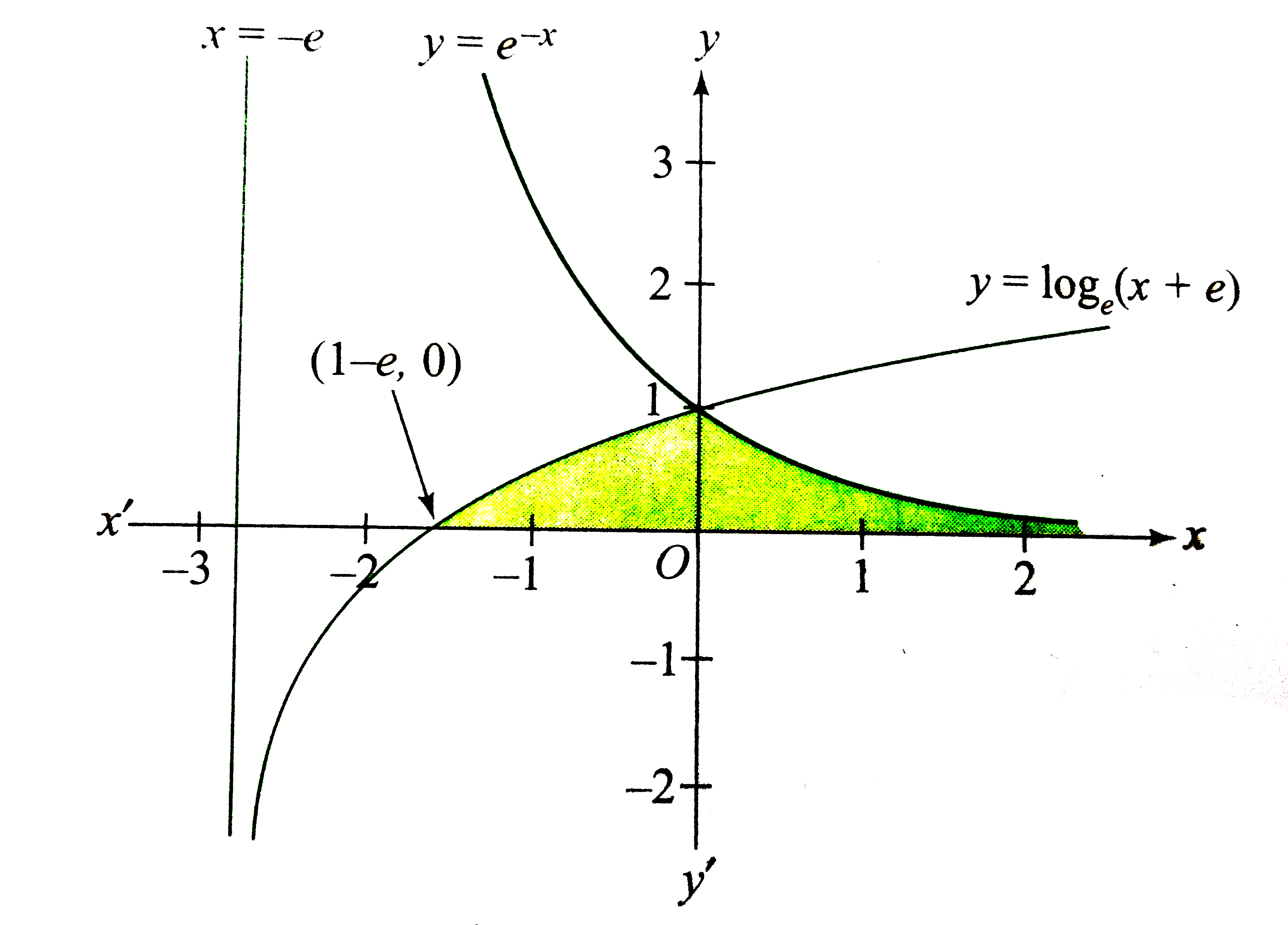
`"Required area "=overset(0)underset(1-e)intlog_(e)(x+e)dx+overset(oo)underset(0)inte^(-x)dx`
`=|x log_(e)(x+e)|_(1-e)^(0)-overset(0)underset(1-e)int(x)/(x+e)dx-|e^(-x)|_(0)^(oo)`
`=overset(1-e)underset(0)int(1-(e)/(x+e))dx-e^(oo)+e^(0)`
`=|x-elog (x+e)|_(0)^(1-e)-0+1`
`=1-e+elog e+1 =2` sq. units.