Find the area bounded by y=1x2−2x+2 and x-axis.
Video Solution
Text Solution
y=1(x−1)2+1
When x=1,ymax .1
When x→±∞,y→0
Therefore, x-axis is the asymptote.
Also f(1+x)=f(1−x)
Hence, the graph is symmetrical about line x = 1
From these information the graph of function is as shown in the figure.
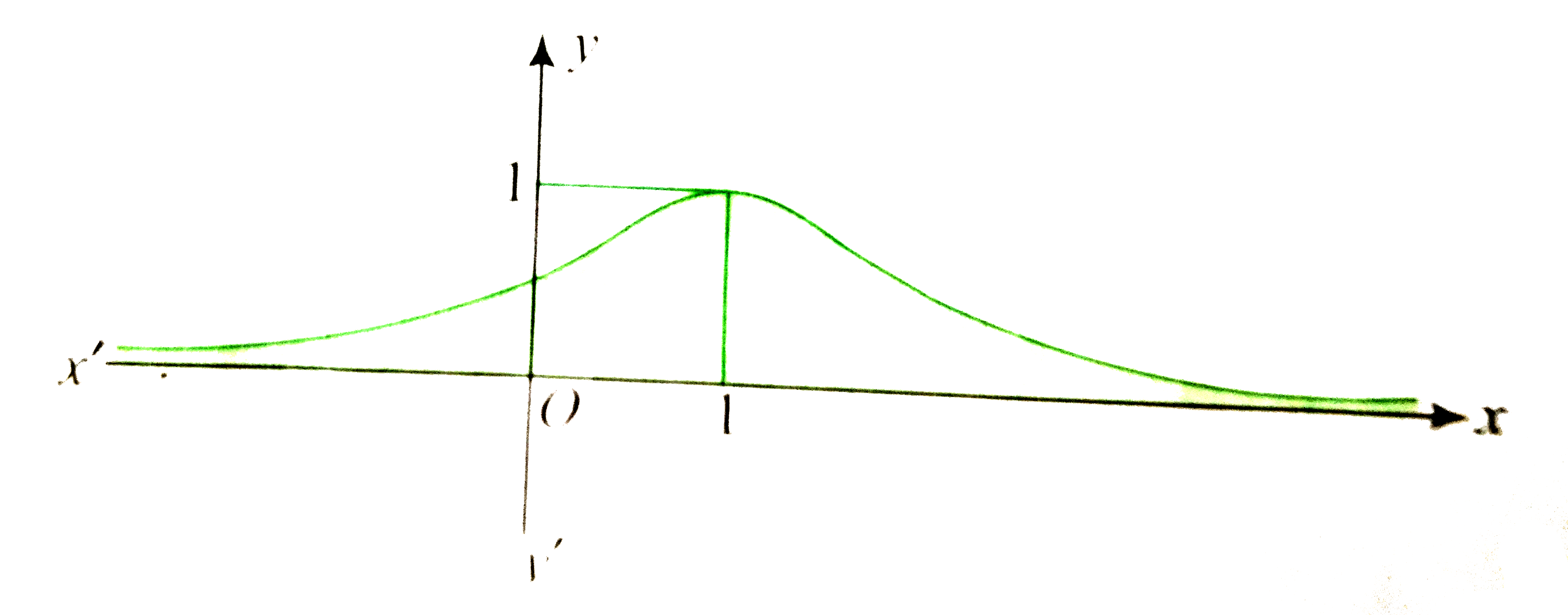
Area =2∞∫11(x−1)2+1dx=[2tan−1(x−1)]∞1=π sq. units.
|
Topper's Solved these Questions
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Solved Examples
10 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Concept Application Exercise 9.1
9 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
Similar Questions
The area bounded by y=1−|x| and X-axis is
View SolutionFind area bounded by y=log12 x and x-axis between x=1 and x=2
View SolutionFind the area bounded by y=1+2sin2x,X-axis,X=0 and x=π.
View SolutionFind the area bounded by the curve y=x3−3x2+2x and the x-axis.
View SolutionFind the area bounded by the curve y=x(x−1)(x−2) and the x-axis.
View Solution∫sinxdx
View SolutionFind the area bounded by the curve |x|+y=1 and axis of x.
View SolutionFind the area bounded by the line y=x, the x-axis and the ordinates x=−1 and x=2
View SolutionFind the area bounded by the line y=x, the x-axis and the ordinates x=−1 and x=2
View SolutionFind the area bounded by curves (x−1)2+y2=1and x2+y2=1.
View Solution
