Number of solutions of the equation, is: (where and greatest integer function) 0 (b) 1 (c) 2 (d)
4
2
3
0
The correct Answer is:D
Also,
From (1) and (2),
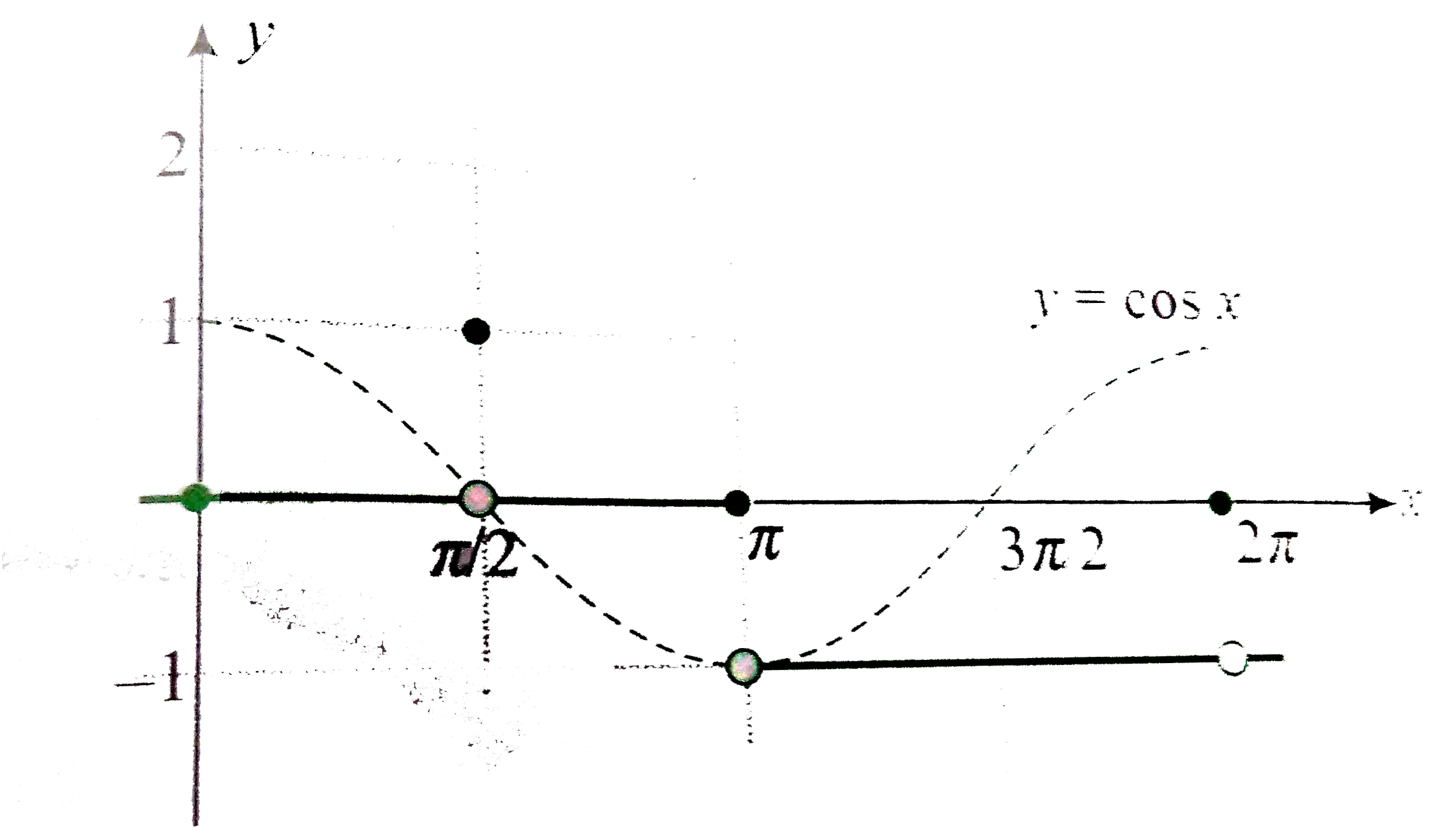
The number of solutions is 0.
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBook:CENGAGE ENGLISHChapter:RELATIONS AND FUNCTIONSExercise:Multiple Correct Answer Type
Explore 27 Videos
- RELATIONS AND FUNCTIONSBook:CENGAGE ENGLISHChapter:RELATIONS AND FUNCTIONSExercise:Linked Comprehension Type
Explore 32 Videos
- RELATIONS AND FUNCTIONSBook:CENGAGE ENGLISHChapter:RELATIONS AND FUNCTIONSExercise:CONCEPT APPLICATION EXERCISE 1.15
Explore 8 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGE ENGLISHChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Archives (Numerical Value Type)
Explore 3 Videos
- SCALER TRIPLE PRODUCTS Book:CENGAGE ENGLISHChapter:SCALER TRIPLE PRODUCTS Exercise:DPP 2.3
Explore 11 Videos
Similar Questions
Number of solutions of the equation, [y+[y]]=2cosx is: (where y=1/3)[sinx+[sinx+[sinx]]] and []= greatest integer function) (a). 0 (b) 1 (c) 2 (d) ∞
View SolutionFind the number of solutions of the equations y=|sinx|andx2+y2=1.
View SolutionThe number of solutions of [sinx+cosx]=3+[−sinx]+[−cosx](where[] denotes the greatest integer function), x∈[0,2π] , is 0 (b) 4 (c) infinite (d) 1
View SolutionGeneral solution of the differential equation (cosx)dydx+y.sinx=1 is
View SolutionThe number of integers in the range of function f(x)=[sinx]+[cosx]+[sinx+cosx] is (where [.]= denotes greatest integer function)
View SolutionThe range of the function f(x)=cosec−1[sinx] in [0,2π], where [⋅] denotes the greatest integer function , is
View SolutionThe number of solutions of the equation |cosx−sinx|=2cosx∈[0,2π] is (A) 1 (B) 2 (C) 3 (D) 4
View SolutionThe number of solution of 2cosx=|sinx| where x∈[0.4π] is/are
View SolutionFind the number of solution of [cosx]+∣sinx=1∈π≤x≤3π where [] denotes the greatest integer function.
View Solutionlimx→π2sinxcos−1[14(3sinx−sin3x)] where [] denotes greatest integer function id:
View Solution
